题目内容
已知正三棱柱ABC-A1B1C1,底面边长为8,对角线B1C=10,
(1)若D为AC的中点,求证:AB1∥平面C1BD;
(2)若CD=2AD,BP=λPB1,当λ为何值时,AP∥平面C1BD;
(3)在(1)的条件下,求直线AB1到平面C1BD的距离.
(1)若D为AC的中点,求证:AB1∥平面C1BD;
(2)若CD=2AD,BP=λPB1,当λ为何值时,AP∥平面C1BD;
(3)在(1)的条件下,求直线AB1到平面C1BD的距离.
分析:(1)连接B1C,设B1C与BC1交于点E,连接DE,则E为B1C中点,利用DE是△CAB1的中位线证出DE∥AB1.
(2)λ=1时,AP∥平面C1BD.连接PC,设PC与BC1交于点F,连接DF.利用CF:FP=CD:AD=2:1.
得出DF∥AP,从而AP∥平面C1BD.
(3)将直线AB1到平面C1BD的距离转化为点A到平面C1BD的距离.利用等体积法求出距离即可.
(2)λ=1时,AP∥平面C1BD.连接PC,设PC与BC1交于点F,连接DF.利用CF:FP=CD:AD=2:1.
得出DF∥AP,从而AP∥平面C1BD.
(3)将直线AB1到平面C1BD的距离转化为点A到平面C1BD的距离.利用等体积法求出距离即可.
解答: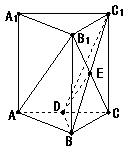 解:(1)连接B1C,设B1C与BC1交于点E,连接DE,
解:(1)连接B1C,设B1C与BC1交于点E,连接DE,
则E为B1C中点,又D为AC的中点,
∴DE是△CAB1的中位线,
∴DE∥AB1,
又DE?平面BDC1,AB1?平面C1BD,
∴AB1∥平面C1BD.
(2)λ=1时,AP∥平面C1BD;
证明如下:连接PC,设PC与BC1交于点F,连接DF.
当λ=1时,P为B1B中点,C1C:PB=CF:FP=2:1,
又CD=2AD,∴CF:FP=CD:AD=2:1.
∴DF∥AP,
又DF?平面BDC1,AP?平面C1BD,
∴AP∥平面C1BD.
(3)由(1)当D为AC的中点时,AB1∥平面C1BD;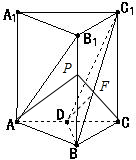
∴点A到平面C1BD的距离等于直线AB1到平面C1BD的距离,记为h.
正三棱柱的高C1C=
=
=6.
由正三棱柱性质可知面CC1⊥面ABC,BD?面ABC,∴CC1⊥BD.
又在正三角形ABC中,D为AB中点,∴AC⊥BD,
∵AC∩CC1=C,∴,BD⊥面A1ACC1,DC1?面A1ACC1,∴BD⊥DC1,
∴△BDC1 是直角三角形.
∵S△ABD=
AD×BD=
AD×
=
×4×
=8
.
C1D=
=
=2
.
∴S△BDC1=
BD×C1D=
×4
×2
=4
.
∵VA-C1BD=VC1-ABD.
∴
S△BDC1=×h=
S△ABD=×C1C
代入数据,得出
×4
×h=
×8
.×6
h=
=
.
∴直线AB1到平面C1BD的距离为
.
 解:(1)连接B1C,设B1C与BC1交于点E,连接DE,
解:(1)连接B1C,设B1C与BC1交于点E,连接DE,则E为B1C中点,又D为AC的中点,
∴DE是△CAB1的中位线,
∴DE∥AB1,
又DE?平面BDC1,AB1?平面C1BD,
∴AB1∥平面C1BD.
(2)λ=1时,AP∥平面C1BD;
证明如下:连接PC,设PC与BC1交于点F,连接DF.
当λ=1时,P为B1B中点,C1C:PB=CF:FP=2:1,
又CD=2AD,∴CF:FP=CD:AD=2:1.
∴DF∥AP,
又DF?平面BDC1,AP?平面C1BD,
∴AP∥平面C1BD.
(3)由(1)当D为AC的中点时,AB1∥平面C1BD;

∴点A到平面C1BD的距离等于直线AB1到平面C1BD的距离,记为h.
正三棱柱的高C1C=
| B1C2- B1C12 |
| 102-82 |
由正三棱柱性质可知面CC1⊥面ABC,BD?面ABC,∴CC1⊥BD.
又在正三角形ABC中,D为AB中点,∴AC⊥BD,
∵AC∩CC1=C,∴,BD⊥面A1ACC1,DC1?面A1ACC1,∴BD⊥DC1,
∴△BDC1 是直角三角形.
∵S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| AB2-AD2 |
| 1 |
| 2 |
| 82-42 |
| 3 |
C1D=
| C1C2+CD2 |
| 62+42 |
| 13 |
∴S△BDC1=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 13 |
| 39 |
∵VA-C1BD=VC1-ABD.
∴
| 1 |
| 3 |
| 1 |
| 3 |
代入数据,得出
| 1 |
| 3 |
| 39 |
| 1 |
| 3 |
| 3 |
h=
| 12 | ||
|
12
| ||
| 13 |
∴直线AB1到平面C1BD的距离为
12
| ||
| 13 |
点评:本题考查直线和平面平行关系的证明与判定,点面距的求解.考查分析、探索、转化、计算论证能力.求点面距的几何法常用两种:直接作出或找出距离,通过解直角三角形解决,或利用等体积转化法.

练习册系列答案
相关题目
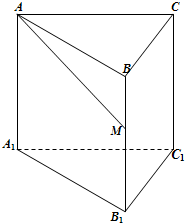 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ. 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.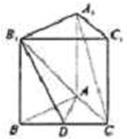 如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1. (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.