��Ŀ����
����Ŀ�����������������о��õĿ��ٷ�չ������������Խ��Խ��ע��������һ������������ε�����![]() ����ͼ��ʾ������߳�Ϊ2���ף�Ϊ������������������������������������㴦�ֱ������ι㳡��������
����ͼ��ʾ������߳�Ϊ2���ף�Ϊ������������������������������������㴦�ֱ������ι㳡��������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() �ֱ������ڵ�
�ֱ������ڵ�![]() ����
����![]() ��
��![]() ���ص���ʣ�ಿ�֣���Ӱ���֣���ֲ��ƺ.��
���ص���ʣ�ಿ�֣���Ӱ���֣���ֲ��ƺ.��![]() ��Ϊ
��Ϊ![]() ����λ�����ף�����ƺ���Ϊ
����λ�����ף�����ƺ���Ϊ![]() ����λ����ƽ���ף�.
����λ����ƽ���ף�.
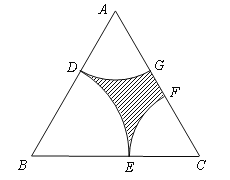
��1������![]() �ֱ��ʾ����
�ֱ��ʾ����![]() ��
��![]() ����������
���������д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() Ϊ��ֵʱ����ƺ���������������.
Ϊ��ֵʱ����ƺ���������������.
���𰸡���1��![]() ��
��![]() ��
��![]() ����2��
����2��![]() ʱ����ƺ������������Ϊ
ʱ����ƺ������������Ϊ![]() ��ƽ����.
��ƽ����.
��������
��1����Ϊ![]() �����Կɵ��������εİ뾶��Բ�ĽǶ�Ϊ
�����Կɵ��������εİ뾶��Բ�ĽǶ�Ϊ![]() �������ε������ʽ�ɵô𰸣�
�������ε������ʽ�ɵô𰸣�
��2���������������ȥ������������ɵò�ƺ����������ö��κ����������ֵ.
��1��![]() ����
����![]() ��
��![]() ��
��
������![]() ��
�У�![]() �ij�Ϊ
�ij�Ϊ![]() ��
��
����![]() ��
��
ͬ����![]() .
.
��![]() ��
��![]() ���ص�����
���ص�����![]() ����
����![]() ����
����![]() .
.
���������ζ����������ڲ�����![]() ����
����![]() .
.
��2����![]() ��
��
��![]()
![]()
 ��
��
�൱![]() ʱ��
ʱ��![]() ȡ�����ֵ��Ϊ
ȡ�����ֵ��Ϊ![]() .
.
�ʵ�![]() ��Ϊ
��Ϊ![]() ����ʱ����ƺ������������Ϊ
����ʱ����ƺ������������Ϊ![]() ��ƽ����.
��ƽ����.

����Ŀ��ij����Ϊ�˽�Ⱥ�����°������ʹ��������������䰴�ֲ�����ķ�ʽ�����˸õ���50��Ⱥ�ڣ����ǵ�����Ƶ����ʹ�ù������������ֲ����±���
����� | 20~29 | 30~39 | 40~49 | 50~60 |
Ƶ�� | 12 | 18 | 15 | 5 |
����ʹ�ù������� | 6 | 12 | 5 | 1 |
��1��������ͳ��������������![]() �����������ж��Ƿ���95%�İ�����Ϊ��40��Ϊ�ֽ����Ƿ�ʹ�ù��������в��죿
�����������ж��Ƿ���95%�İ�����Ϊ��40��Ϊ�ֽ����Ƿ�ʹ�ù��������в��죿
�������40�� | ���䲻����40�� | �ܼ� | |
����ʹ�ù������� | |||
������ʹ�ù������� | |||
�ܼ� |
����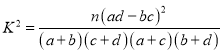 ��
��![]() .
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
��2�������÷ֲ�����ķ�ʽ���������40���Ҿ���ʹ�ù���������Ⱥ����ѡ��6�ˣ��ٴ���6���������ȡ2�ˣ�����2����ǡ����1��������30~39��ĸ���.
