题目内容
【题目】某地区为了解群众上下班共享单车使用情况，根据年龄按分层抽样的方式调查了该地区50名群众，他们的年龄频数及使用共享单车人数分布如下表：
年龄段 | 20~29 | 30~39 | 40~49 | 50~60 |
频数 | 12 | 18 | 15 | 5 |
经常使用共享单车 | 6 | 12 | 5 | 1 |
（1）由以上统计数据完成下面的
列联表，并判断是否有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异？
年龄低于40岁 | 年龄不低于40岁 | 总计 | |
经常使用共享单车 | |||
不经常使用共享单车 | |||
总计 |
附：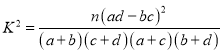
，
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
（2）若采用分层抽样的方式从年龄低于40岁且经常使用共享单车的群众中选出6人，再从这6人中随机抽取2人，求这2人中恰好有1人年龄在30~39岁的概率.
【答案】(1)见解析;(2)
【解析】
（1）根据题意填写列联表,由表中数据计算观测值,对照临界值得出结论；
（2）用分层抽样法选出6人,利用列举法求出基本事件数,再计算所求的概率值.
(1) 根据题意填写2×2列联表如下:
年龄低于40岁 | 年龄不低于40岁 | 总计 | |
经常使用共享单车 | 18 | 6 | 24 |
不经常使用共享单车 | 12 | 14 | 36 |
总计 | 30 | 20 | 50 |
由表中数据,计算
所以没有95%的把握认为以40岁为分界点对是否经常使用共享单车有差异.
(2) 用分层抽样法选出6人,其中20~29岁的有2人,记为A、B，30~39岁的有4人,记为c、d、e、f,再从这6人中随机抽取2人,基本事件为: AB、Ac、Ad、Ae、Af、Be、Bd、Be、Bf、cd、ce、cf、de、df、ef共15种不同取法；则抽取的这2人中恰好有1人年龄在30~39岁的基本事件为:Ac、Ad、Ae、Af、Bc、Bd、Be、Bf共8种不同取法;
故所求的概率为
.
