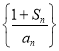题目内容
【题目】已知![]() ,设函数
,设函数![]() ,
,![]() .
.
(1)试讨论![]() 的单调性;
的单调性;
(2)设函数![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,且满足
,且满足![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
注:![]() .
.
【答案】(1)答案不唯一,见解析;(2)存在,![]()
【解析】
(1)求出函数的定义域以及![]() ,讨论
,讨论![]() 的取值范围,即
的取值范围,即![]() ,
,![]() ,
,![]() 或
或![]() ,利用导数与函数单调性的关系即可求解.
,利用导数与函数单调性的关系即可求解.
(2)解法一:求出![]() ,根据题意可得
,根据题意可得![]() 有两解两解
有两解两解![]() ,从而可得
,从而可得![]() ,从而求得
,从而求得![]() ,由
,由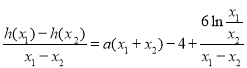 ,令
,令![]() ,可得
,可得![]() ,利用导数求出
,利用导数求出![]() 的单调性,且根据
的单调性,且根据![]() 即可求解;解法二:根据函数有两个极值点可得
即可求解;解法二:根据函数有两个极值点可得![]() ,然后将不等式化为
,然后将不等式化为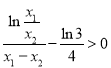 ,由方程
,由方程![]() ,得
,得![]() ,令
,令![]() ,
,![]() ,则
,则![]() ,将不等式化为关于
,将不等式化为关于![]() 的不等式,利用导数即可证出.
的不等式,利用导数即可证出.
解:(1)![]() 的定义域为
的定义域为![]()
![]() =
=![]() =
=![]() ,
,
(i)若![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 递增,
递增,![]() 递减,
递减,
(ii)若![]() ,则
,则![]() 在
在![]() 递增,
递增,![]() 递减,在
递减,在![]() 递增,
递增,
(iii)若![]() ,则
,则![]() 在
在![]() 递增;
递增;
(iv)若![]() ,则
,则![]() 在
在![]() 递增,在
递增,在![]() 递减,在
递减,在![]() 递增.
递增.
(2)解法一: ![]() ,
,![]()
![]()
![]() , 若
, 若![]() 有两极值点,
有两极值点,
则![]() 有两解两解
有两解两解![]() ,
,
![]() .
.
且![]()
所以![]() .
.
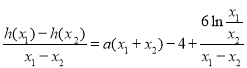
令![]() ,则
,则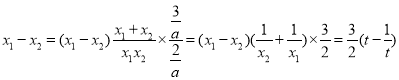
![]()
若![]() 则
则![]() ,
,
![]() ,
,
令![]()
![]() ,
,![]()
![]() ,
,![]()
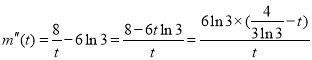
所以![]() 在
在![]() 递增,在
递增,在![]() 递减
递减
又![]() ,
,![]()
则在区间![]() 内存在
内存在![]() 使得
使得![]() .
.
函数y=m(x)在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
由![]() ,所以当
,所以当![]() 时满足
时满足![]()
 ,所以
,所以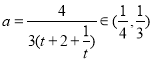
即实数![]() 的取值范围为
的取值范围为![]()
解法二: ![]() ,
,![]()
![]()
![]() , 若
, 若![]() 有两极值点,
有两极值点,
则![]() 有两解
有两解![]() ,
,
![]()
且![]() ,所以
,所以![]()
![]()
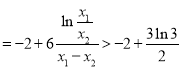
即 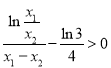
由方程![]() ,得
,得![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
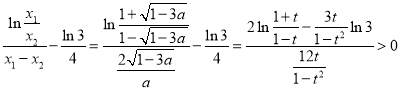
令![]() ,求导可得
,求导可得
![]()
![]() .
.
令![]() ,得到
,得到![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减.
单调递减.
又![]() ,
, ,所以由
,所以由![]() ,
,
即![]() ,解得
,解得![]() . 故实数
. 故实数![]() 的取值范围是
的取值范围是![]() .
.

【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(i)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
(命题意图)本题主要考查给出样本频数分别表求样本的均值、将频率做概率求互斥事件的和概率,是简单题.