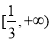题目内容
2.已知点F($\sqrt{3}$,0),圆E:(x+$\sqrt{3}$)2+y2=16,点P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.(1)求动点Q的轨迹方程;
(2)若直线l与圆O:x2+y2=1相切,并与(1)中轨迹交于不同的两点A、B.当$\overrightarrow{OA}$•$\overrightarrow{OB}$=λ,且满足$\frac{1}{2}$≤λ≤$\frac{2}{3}$时,求△AOB面积S的取值范围.
分析 (1)连接QF,结合圆的定义和垂直平分线的性质,以及椭圆的定义,可得Q的轨迹方程;
(2)设直线l的方程为x=my+n(m∈R),由直线和圆相切的条件:d=r,可得m,n的关系,联立直线方程和椭圆方程,运用韦达定理和弦长公式,求得△AOB的面积,结合向量的数量积的坐标表示和基本不等式,即可得到所求范围.
解答 解:(1)连接QF,∵|QE|+|QF|=|QE|+|QP|=|PE|=4>|EF|=2$\sqrt{3}$,
∴动点Q的轨迹是以E(-$\sqrt{3}$,0)、F($\sqrt{3}$,0)为焦点,长轴长2a=4的椭圆,
即动点Q的轨迹方程为:$\frac{{x}^{2}}{4}$+y2=1;
(2)依题结合图形知直线l的斜率不为零,
所以设直线l的方程为x=my+n(m∈R).
∵直线L即x-my-n=0与圆O:x2+y2=1相切,
∴$\frac{|n|}{\sqrt{{m}^{2}+1}}$=1得n2=m2+1.
又∵点A,B的坐标满足:$\left\{\begin{array}{l}{x=my+n}\\{{x}^{2}+4{y}^{2}-4=0}\end{array}\right.$,
消去x整理得(m2+4)y2+2mny+n2-4=0,
由韦达定理得y1+y2=-$\frac{2mn}{4+{m}^{2}}$,y1y2=$\frac{{n}^{2}-4}{4+{m}^{2}}$,
又|AB|=$\sqrt{1+{m}^{2}}$•|y1-y2|,点O到直线l的距离d=$\frac{|n|}{\sqrt{1+{m}^{2}}}$=1,
∴S△AOB=$\frac{1}{2}$d•|AB|=$\frac{1}{2}$$\sqrt{1+{m}^{2}}$•|y1-y2|=$\frac{1}{2}$|n|•|y1-y2|
=2$\sqrt{3}$•$\sqrt{\frac{{n}^{2}}{({m}^{2}+4)^{2}}}$=2$\sqrt{3}$•$\sqrt{\frac{1+{m}^{2}}{({m}^{2}+4)^{2}}}$,
∵λ=$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=(my1+n)(my2+n)+y1y2
=(m2+1)y1y2+mn(y1+y2)+n2=$\frac{5{n}^{2}-4{m}^{2}-4}{4+{m}^{2}}$=$\frac{{m}^{2}+1}{4+{m}^{2}}$
∵$\frac{1}{2}≤λ≤\frac{2}{3}$,令t=1+m2,则λ=$\frac{t}{3+t}$∈[$\frac{1}{2}$,$\frac{2}{3}$],即有t∈[3,6]
∴S△AOB=2$\sqrt{3}$•$\sqrt{\frac{1+{m}^{2}}{({m}^{2}+4)^{2}}}$=2$\sqrt{3}$•$\sqrt{\frac{t}{(t+3)^{2}}}$=2$\sqrt{3}$•$\sqrt{\frac{t}{{t}^{2}+6t+9}}$=$\frac{2\sqrt{3}}{\sqrt{t+\frac{9}{t}+6}}$
∵t+$\frac{9}{t}$∈[6,$\frac{15}{2}$],t+$\frac{9}{t}$+6∈[12,$\frac{27}{2}$],$\sqrt{t+\frac{9}{t}+6}$∈[$\sqrt{12}$,$\sqrt{\frac{27}{2}}$],
∴S△AOB∈[$\frac{2\sqrt{2}}{3}$,1],∴S△AOB的取值范围为[$\frac{2\sqrt{2}}{3}$,1].
点评 本题考查椭圆的定义、方程和性质,主要考查椭圆的定义和方程的运用,联立直线方程,运用韦达定理,弦长公式和基本不等式,属于中档题.

| A. | -log32 | B. | log32 | C. | -log23 | D. | log23 |

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
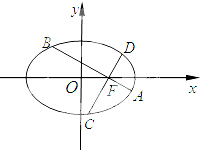 如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.
如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.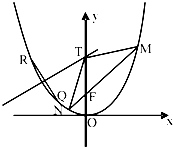 如图,过抛物线C:x2=2py(p>0)的焦点F的直线交C于M(x1,y1),N(x2,y2)两点,且x1x2=-4.
如图,过抛物线C:x2=2py(p>0)的焦点F的直线交C于M(x1,y1),N(x2,y2)两点,且x1x2=-4.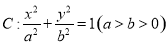 的左、右焦点分别为
的左、右焦点分别为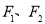 ,椭圆
,椭圆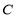 过点
过点 ,直线
,直线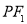 交
交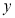 轴于
轴于 ,且
,且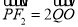 ,
,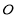 为坐标原点.
为坐标原点. 的方程;
的方程;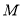 是椭圆
是椭圆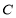 的上顶点,过点
的上顶点,过点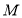 分别作直线
分别作直线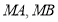 交椭圆
交椭圆 于
于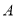 ,
,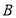 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线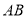 过定点.
过定点. 的定义域为( )
的定义域为( )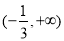 B.
B.
 D.
D.