题目内容
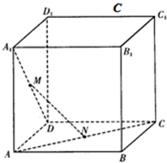 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.(1)求异面直线MN和AB所成的角;
(2)求点M到平面BB1D1D之距.
分析:(1)可以先求出MN和CD所成的角为45°,然后由CD∥AB即可求出MN和AB所成的角;
(2)先求出A1和平面BB1D1D的距离,M点到平面BB1D1D的距离为 A1和平面BB1D1D的距离的二分之一
(2)先求出A1和平面BB1D1D的距离,M点到平面BB1D1D的距离为 A1和平面BB1D1D的距离的二分之一
解答:解:(1)在正方体ABCD-A1B1C1D1中,M为A1D中点,
连接AD1,则M为A1D和AD1的交点
在△AD1C中,M、N分别为AD1和AC之中点,
∴MN∥D1C,而D1C和DC所成角为45°,又DC∥AB
∴MN和AB所在异面角为45°.
(2)∵在正方体ABCD-A1B1C1D1中,BDD1B1为体对角面
∴A1到面BD1之距即A1到B1D1之距
a.
又M为A1D之中点,从而M到BD1之距
a.
连接AD1,则M为A1D和AD1的交点
在△AD1C中,M、N分别为AD1和AC之中点,
∴MN∥D1C,而D1C和DC所成角为45°,又DC∥AB
∴MN和AB所在异面角为45°.
(2)∵在正方体ABCD-A1B1C1D1中,BDD1B1为体对角面
∴A1到面BD1之距即A1到B1D1之距
| ||
| 2 |
又M为A1D之中点,从而M到BD1之距
| ||
| 4 |
点评:此题考查异面直线所成的角的求法和点到平面距离的求法,解题时要注意数形结合的数学思想的运用,有一定的技巧,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( ) ,当
,当 取什么位置时,三棱柱的体积最大?
取什么位置时,三棱柱的体积最大?





