Question

如图，在棱长为2的正四面体A-BCD中，若以△ABC为视角正面，则其正视图的面积是（　　）

• A．

  3

• B．

  2

  3

  6

• C．2

  3

• D．

  11

  3

Answer 1

分析：正视图是一个三角形，底边长是等于棱长2，高为正四面体A-BCD的高的一个等腰三角形，即可判断三角形的形状，然后求出面积即可．

解答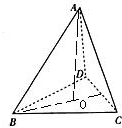：解：由题意可知：正视图是一个三角形，底边长是等于棱长2，高为正四面体A-BCD的高的一个等腰三角形，
∵正四面体的棱长为：2，
底面三角形的高：

3

，
棱锥的高为：

22-( 2 3 × 3 ) 2

=

2 6

3

即正视图是一个三角形，底边长是等于棱长2，高为

2 6

3

一个等腰直角三角形．
面积为：

1

2

×2×

2 6

3

= 

2 6

3

，
故选B．

点评：本题考查简单几何体的三视图，考查空间想象能力，计算能力，是基础题．