题目内容
如图,在所有棱长为a的正三棱柱ABC—A1B1C1中,D为BC的中点.
(1)求证:AD⊥BC1;
(2)求二面角ABC1D的大小;
(3)求点B1到平面ABC1的距离.
(1)证明:在正三棱柱ABC—A1B1C1中,CC1⊥面ABC,
 AD⊥BC1.
AD⊥BC1.
(2)解:过D作DE⊥BC1于E,连结AE,
由(1)知AD⊥面BC1CB,
∴AE在面BB1C1C上的射影是DE.故AE⊥BC1.
∴∠AED为二面角A-BC1-D的平面角.
依题设BC1=![]() a,故在△BC1D中,
a,故在△BC1D中,
DE=![]() .
.
又AD=![]() a,在Rt△ADE中,tan∠AED=
a,在Rt△ADE中,tan∠AED=![]() ,
,
∴二面角A-BC1-D的大小为arctan![]() .
.
(3)解:依题意,AC1=BC1=![]() a,取AB的中点F,连结C1F,则C1F=
a,取AB的中点F,连结C1F,则C1F=![]() a.设B1到平面ABC1的距离为d,则由
a.设B1到平面ABC1的距离为d,则由![]() ,
,
得![]()
![]() ·d=
·d=![]() ·AD,
·AD,
即![]() ·a·
·a·![]() a·d=
a·d=![]() ·a·
·a·![]() a.
a.
∴d=![]() a,即B1到平面ABC1的距离为
a,即B1到平面ABC1的距离为![]() a.
a.

练习册系列答案
相关题目
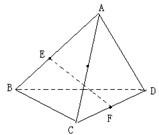 如图,在四面体ABCD中,已知所有棱长都为a,点E、F分别是AB、CD的中点.
如图,在四面体ABCD中,已知所有棱长都为a,点E、F分别是AB、CD的中点.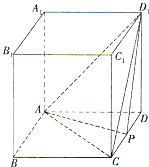 如图,正方体ABCD-A1B1C1D1的棱长为2,P为棱CD上的一点,且三棱锥A-CP D1的体积为
如图,正方体ABCD-A1B1C1D1的棱长为2,P为棱CD上的一点,且三棱锥A-CP D1的体积为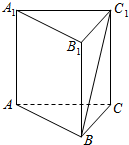 如图,在三棱柱ABC-A1B1C1中,所有棱长都相等,且AA1⊥底面ABC,则BC1与平面ACC1A1所成角的余弦值为( )
如图,在三棱柱ABC-A1B1C1中,所有棱长都相等,且AA1⊥底面ABC,则BC1与平面ACC1A1所成角的余弦值为( )