题目内容
已知四棱锥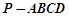 的底面是平行四边形,
的底面是平行四边形,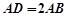 ,
,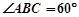 ,
,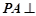 面
面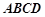 ,
,
且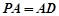 .若
.若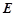 为
为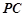 中点,
中点,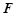 为线段
为线段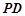 上的点,且
上的点,且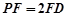 .
.
(1)求证: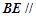 平面
平面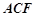 ;
;
(2)求PC与平面PAD所成角的正弦值.
 的底面是平行四边形,
的底面是平行四边形,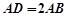 ,
,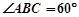 ,
,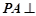 面
面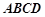 ,
,且
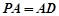 .若
.若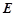 为
为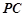 中点,
中点,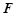 为线段
为线段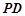 上的点,且
上的点,且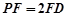 .
.(1)求证:
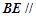 平面
平面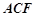 ;
;(2)求PC与平面PAD所成角的正弦值.

 |
(1)详见解析;(2)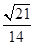 .
.
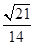 .
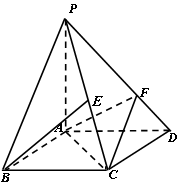
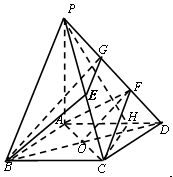
.试题分析:(1)连结BD交AC于O,取PF中点G,连结OF,BG,EG,利用EO,EG分别为BG,FC的中位线,得到它们对应平行,进而得到平面BEG与平面ACF平行,再由面面平行的性质得到线面平行.
(2)要求线面角,需要先找到线面角的代表角,即过C点做面PAD的垂线,因为PA垂直于底面,所以过C作线段AD的垂线与AD交于H,则CH垂直于面PAD,所以角CPH即为线面角的代表角,要求该角的正弦值,就需要求出PC与CH,可以利用△PAC和△ACH为直角三角形通过勾股定理求出,进而得到线面角的正弦值.
解:(1)证明1:连接BD交AC于点O,取
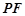 中点
中点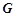 ,连接
,连接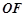 、
、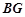 、
、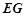 .
.
因为
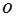 、
、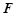 分别是
分别是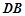 、
、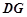 的中点, 所以
的中点, 所以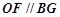 ,
, 又
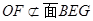 ,所以
,所以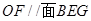 2分
2分因为
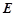 、
、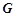 分别是
分别是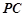 、
、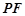 的中点,
的中点,所以
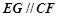 ,同理可得
,同理可得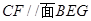 4分
4分又
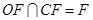 所以,平面
所以,平面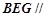 平面
平面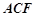 .
.又因为
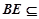 平面
平面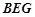 ,故
,故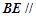 平面
平面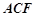 . 6分
. 6分证明2:作AH垂直BC交BC于H
建立如图的空间直角坐标系O-XYZ,
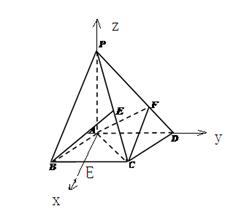
令AD=PA=2,则AB=1
所以

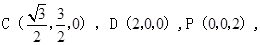
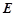 为
为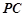 中点,
中点, 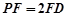 所以
所以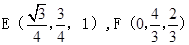 2分
2分设面AFC的一个法向量
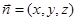 ,又
,又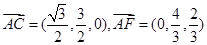
由
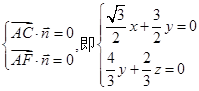 ,
,所以
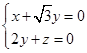
令
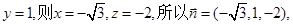 4分
4分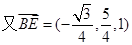 所以
所以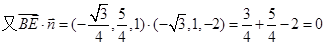
所以
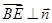 故
故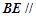 平面
平面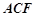 . 6分
. 6分(2)解1:因为
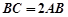 ,
,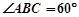 ,所以
,所以 .
.过C作AD的垂线,垂足为H,则
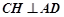 ,
,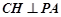 ,所以
,所以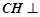 平面PAD.
平面PAD.故
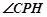 为PC与平面PAD所成的角. 9分
为PC与平面PAD所成的角. 9分设
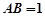 ,则
,则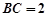 ,
,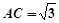 ,
,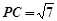 ,
,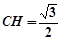
所以
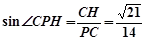 ,即为所求. 12分
,即为所求. 12分解2:作AH垂直BC交BC于H,建立如图的空间直角坐标系O-XYZ,
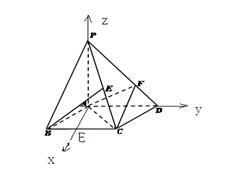
令AD=PA=2,则AB=1,
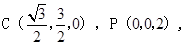 所以
所以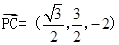 8分
8分因为
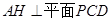 ,所以面PCD的一个法向量为
,所以面PCD的一个法向量为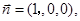 10分
10分令PC与平面PAD所成的角为
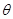 ,则
,则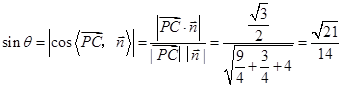 故PC与平面PAD所成角的正弦值为
故PC与平面PAD所成角的正弦值为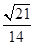 . 12分.
. 12分.
练习册系列答案
相关题目
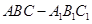 中,侧棱
中,侧棱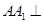 平面
平面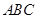 ,
,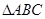 为等腰直角三角形,
为等腰直角三角形,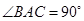 ,且
,且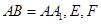 分别是
分别是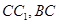 的中点.
的中点.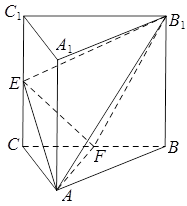
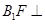 平面
平面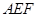 ;
;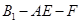 的余弦值.
的余弦值.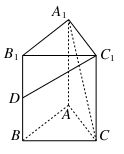
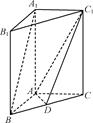
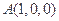 的距离除以到
的距离除以到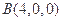 的距离的值为
的距离的值为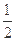 的点
的点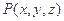 的坐标满足( )
的坐标满足( )