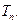题目内容
(本题满分12分)设数列 的前
的前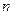 项和为
项和为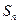 ,对
,对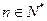 ,都有
,都有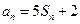 成立,
成立,
(Ⅰ) 求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 ,试求数列
,试求数列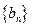 的前
的前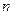 项和
项和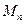 .
.
 的前
的前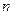 项和为
项和为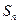 ,对
,对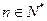 ,都有
,都有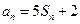 成立,
成立,(Ⅰ) 求数列
 的通项公式;
的通项公式;(Ⅱ)设数列
 ,试求数列
,试求数列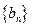 的前
的前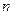 项和
项和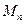 .
.(1)

(2)

解: (Ⅰ)当 时,
时, ,∴
,∴ .
.
当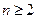 时,
时,

 即
即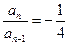 ………… 3分
………… 3分
∴数列 成等比数列,其首项
成等比数列,其首项 ,公比为
,公比为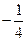
 数
数 列
列 的通项公式
的通项公式 . …………6分
. …………6分
(Ⅱ)由(Ⅰ)知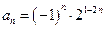 ,
, . …………9分
. …………9分
 为等差数列,且首
为等差数列,且首 相为
相为 ,公差为
,公差为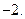
 ………… 12分
………… 12分
 时,
时, ,∴
,∴ .
.当
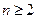 时,
时,

 即
即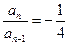 ………… 3分
………… 3分∴数列
 成等比数列,其首项
成等比数列,其首项 ,公比为
,公比为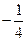
 数
数 列
列 的通项公式
的通项公式 . …………6分
. …………6分(Ⅱ)由(Ⅰ)知
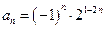 ,
, . …………9分
. …………9分 为等差数列,且首
为等差数列,且首 相为
相为 ,公差为
,公差为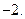
 ………… 12分
………… 12分
练习册系列答案
相关题目
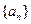 的前n项和为
的前n项和为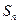 ,
,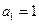 ,
, ,等差数列
,等差数列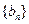 中,
中,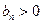
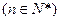 ,且
,且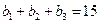 ,又
,又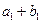 、
、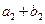 、
、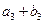 成等比数列.
成等比数列.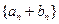 的前n项和Tn.
的前n项和Tn.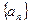 的公差
的公差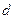 大于0,且
大于0,且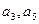 是方程
是方程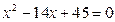 的两根,数列
的两根,数列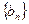 的前
的前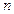 项的和为
项的和为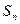 ,且
,且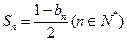 .
.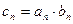 ,求证:
,求证: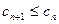 ;
;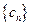 的前
的前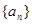 是等差数列,且
是等差数列,且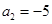 ,
,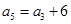 ,则
,则
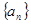 的前n项和为
的前n项和为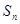 ,若
,若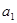 =11,且
=11,且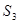 =27,则当
=27,则当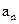 ﹜中,
﹜中, =
=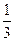 ,前n项和
,前n项和 满足
满足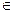 N*
N* )
)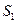 ,t(
,t(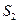 ), 3(
), 3(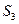 )成等差数列,求实数t的值。
)成等差数列,求实数t的值。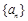 为等比数列,且
为等比数列,且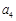 是
是 与
与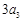 的等差中项,若
的等差中项,若 ,则该数列的前5项的和为 ( )
,则该数列的前5项的和为 ( )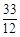

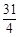
 表示第
表示第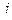 行第
行第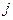 列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列
列的数字,这15个数字中恰有1,2,3,4,5各3个。按预定规则取出这些数字中的部分或全部,形成一个数列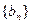 。规则如下:(1)先取出
。规则如下:(1)先取出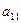 ,并记
,并记 ;若
;若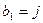 ,则从第
,则从第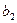 ;(2)以此类推,当
;(2)以此类推,当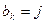 时,就从第
时,就从第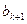 ;直到无法进行就终止。例如由(表(2)可以得到数列
;直到无法进行就终止。例如由(表(2)可以得到数列 ,5,3,2,5,1,3,1. 试问数列
,5,3,2,5,1,3,1. 试问数列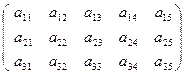
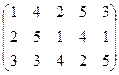
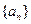 的公差
的公差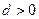 ,其前n项和为
,其前n项和为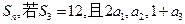 成等比数列。
成等比数列。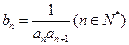 ,求数列
,求数列 的前n项和
的前n项和