题目内容
设等差数列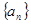 的前n项和为
的前n项和为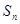 ,若
,若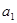 =11,且
=11,且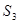 =27,则当
=27,则当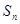 取得最大值时,n的值是( )
取得最大值时,n的值是( )
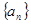 的前n项和为
的前n项和为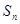 ,若
,若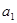 =11,且
=11,且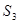 =27,则当
=27,则当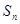 取得最大值时,n的值是( )
取得最大值时,n的值是( ) | A.5 | B. 6 | C. 7 | D.8 |
B
专题:计算题.
分析:求Sn最大值可从两个方面考虑:一是函数方面,等差数列的前n项和是不含常数的二次函数,故可应用二次函数性质求解,要注意n∈N*;二是从Sn的最大值的意义入手,即所以正数项的和最大,故只需通项公式来寻求an≥0,an+1≤0的n
解答:解:∵s3=3a1+3d=27,a1=11
∴d=-2
(法一)∴sn=na1+
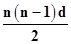 =-n2+12n=-(n-6)2+36
=-n2+12n=-(n-6)2+36∴由二次函数的性质可知,当n=6时Sn最大
(法二)由a1=11>0,d=-2<0
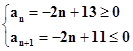 可得
可得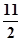 ≤n≤
≤n≤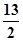 ,n∈N*
,n∈N*当n=6时,Sn最大
故选B
点评:本题主要考查了等差数列的好的最值的求解,数列是一类特殊的函数,在有关的最值的求解中,要善于利用这一性质进行求解,但要注意n为正整数的限制条件.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
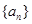 满足
满足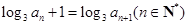 且
且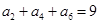 ,则
,则 的值是
的值是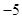
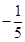
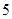
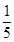
 的前
的前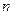 项和为
项和为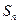 ,对
,对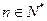 ,都有
,都有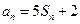 成立,
成立, ,试求数列
,试求数列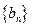 的前
的前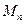 .
.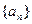 满足:
满足: 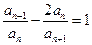 (
(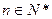 ),且
),且
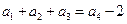 .
. Ⅱ)证明:
Ⅱ)证明: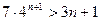 (
( ,设数列
,设数列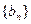 的前
的前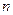 项和为
项和为 (
(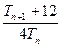 与
与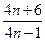 的大小.
的大小.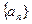 是等差数列,
是等差数列,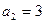 ,
,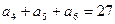 ,
,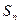 为数列
为数列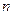 项和
项和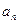 和
和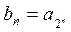 ,求数列
,求数列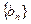 的前
的前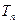
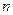 行有
行有
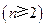 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如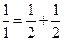 ,
, ,
,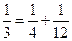 ,…,则第7行第4个数(从左往右数)为( )
,…,则第7行第4个数(从左往右数)为( )
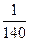
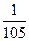
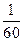
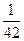
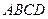 分割成
分割成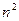
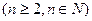 个全等的小正方形(图1,图2分别给出了
个全等的小正方形(图1,图2分别给出了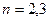 的情形),在每个小正方形的顶点各放置一个数,使位于正方形
的情形),在每个小正方形的顶点各放置一个数,使位于正方形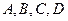 处的四个数互不相同且和为1,记所有顶点上的数之和为
处的四个数互不相同且和为1,记所有顶点上的数之和为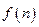 ,则
,则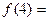
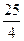 .
.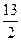
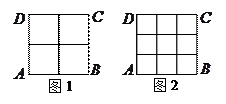
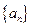 中,
中, ,数列
,数列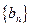 是等比数列,且
是等比数列,且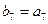 ,则
,则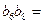 ____
____