题目内容

【题目】在平面直角坐标系xOy中．点M不与点O重合，称射线OM与圆x2+y2=1的交点N为点M的“中心投影点“． ⑴点M（1， ）的“中心投影点”为
⑵曲线x2 上所有点的“中心投影点”构成的曲线的长度是 ．

【答案】["（ ， ）",""]
【解析】解：（1）由题意可得射线OM方程为y= x（x＞0）与圆x2+y2=1

联立，解得x= ，y= ，即有N（ ， ）；（2）双曲线x2 的渐近线方程为y=± x，

代入圆x2+y2=1可得四个交点（ ， ），（﹣ ， ），（﹣ ，﹣ ），（ ，﹣ ）；

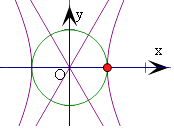
即有曲线x2 上所有点的“中心投影点”构成的曲线为两段圆弧，

且圆心角为120°，半径为1，则弧长为 ．

所以答案是：（1）（ ， ）；（2） ．

练习册系列答案
相关题目

【题目】已知函数 ，其中a∈R． （Ⅰ）给出a的一个取值，使得曲线y=f（x）存在斜率为0的切线，并说明理由；
（Ⅱ）若f（x）存在极小值和极大值，证明：f（x）的极小值大于极大值．

【题目】已知函数f（x）=lnx﹣x+m（m∈R）的图象与x轴相交于A（x1 ， 0），B（x2 ， 0）两点，且x1＜x2 ．
（I）若函数f（x）的最大值为2，求m的值；
（Ⅱ）若 恒成立，求实数k的取值范围；
（Ⅲ）证明：x1x2＜1．

【题目】已知数列{an}的前n项和为Sn（n∈N*），满足Sn=2an﹣1．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足 ，求数列{bn}的前n项和Tn ．

【题目】已知动点M到点N（1，0）和直线l：x=﹣1的距离相等． （Ⅰ）求动点M的轨迹E的方程；
（Ⅱ）已知不与l垂直的直线l'与曲线E有唯一公共点A，且与直线l的交点为P，以AP为直径作圆C．判断点N和圆C的位置关系，并证明你的结论．

【题目】已知椭圆C： ，点P（4，0），过右焦点F作与y轴不垂直的直线l交椭圆C于A，B两点． （Ⅰ）求椭圆C的离心率；
（Ⅱ）求证：以坐标原点O为圆心与PA相切的圆，必与直线PB相切．

【题目】已知椭圆C：x2+4y2=4．
（1）求椭圆C的离心率；
（2）椭圆C的长轴的两个端点分别为A，B，点P在直线x=1上运动，直线PA，PB分别与椭圆C相交于M，N两个不同的点，求证：直线MN与x轴的交点为定点．

【题目】已知 为自然对数的底数，若对任意的 ，总存在唯一的 ，使得 成立，则实数 的取值范围是（ ）
A.
B.
C.
D.

【题目】已知f（x）是定义在R上的偶函数，且f（x+2）=f（x）对x∈R恒成立，当x∈[0，1]时，f（x）=2x ， 则f（﹣log224）= ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网