题目内容
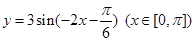 的单调递增区间是( )
的单调递增区间是( )A、
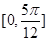 B、
B、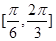 C、
C、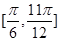 D、
D、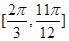
B
由已知中函数的解析式,我们可利用诱导公式,将函数解析式的ω值化为正,进而根据正弦型函数的单调区间的确定方法,即可得到函数的单调区间,再由已知中自变量的取值范围,即可得到答案.
解:∵函数y=3sin(-2x- ) =y=3sin[π-(-2x-
) =y=3sin[π-(-2x- ) ]=3sin(2x+
) ]=3sin(2x+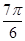 )
)
令-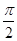 +2kπ≤2x+
+2kπ≤2x+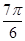 ≤
≤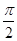 +2kπ,k∈Z
+2kπ,k∈Z
解得-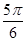 +kπ≤x≤-
+kπ≤x≤-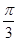 +kπ,k∈Z
+kπ,k∈Z
又∵x∈[0,π]
∴k=1时
x∈[ ,
,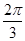 ]
]
故答案为:B
考查的知识点是正弦函数的单调性,其中将利用诱导公式,将解析式中A,ω均化为正数是解答此类问题的关键
解:∵函数y=3sin(-2x-
 ) =y=3sin[π-(-2x-
) =y=3sin[π-(-2x- ) ]=3sin(2x+
) ]=3sin(2x+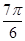 )
) 令-
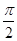 +2kπ≤2x+
+2kπ≤2x+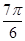 ≤
≤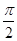 +2kπ,k∈Z
+2kπ,k∈Z解得-
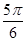 +kπ≤x≤-
+kπ≤x≤-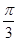 +kπ,k∈Z
+kπ,k∈Z又∵x∈[0,π]
∴k=1时
x∈[
 ,
,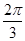 ]
]故答案为:B
考查的知识点是正弦函数的单调性,其中将利用诱导公式,将解析式中A,ω均化为正数是解答此类问题的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
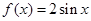 图象按向量
图象按向量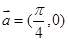 平移得函数
平移得函数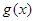 的图象,则函数
的图象,则函数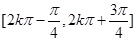 (
(  )
) (
(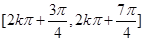 (
(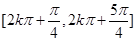 (
( 角
角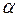 是第三象限角,且
是第三象限角,且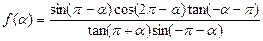
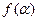 ;
;  2)若
2)若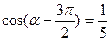 ,求
,求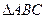 中,角
中,角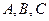 的对边分别为
的对边分别为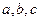 .
. 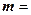
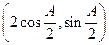 ,
,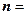
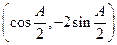 ,.
,.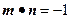
 的值;
的值;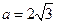 ,
, 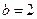 , 求
, 求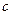 的值.
的值.  对称的是()
对称的是()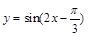


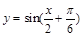
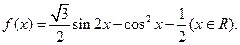
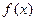 的最小值和最小正周期;
的最小值和最小正周期;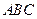 的内角
的内角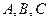 对边分别为
对边分别为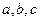 ,且
,且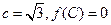 ,
,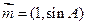 与
与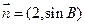 共线,求
共线,求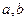 的值.
的值.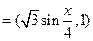 ,n
,n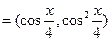 ,函数
,函数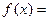 m·n.
m·n.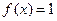 ,求
,求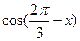 的值;
的值;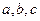 ,且满足
,且满足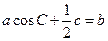 ,求
,求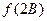
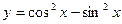 的周期是___________
的周期是___________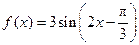 的图象为
的图象为 ,则如下结论中正确的序号是 _____
,则如下结论中正确的序号是 _____ 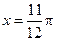 对称;
对称; 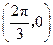 对称;
对称; 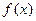 在区间
在区间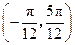 内是增函数;
内是增函数; 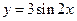 的图角向右平移
的图角向右平移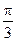 个单位长
个单位长 度可以得到图象
度可以得到图象