题目内容
1.已知正方体的全面积为24cm2:(1)求该正方体的内切球的体积;
(2)求该正方体的外接球的体积.
分析 (1)根据已知中正方体的全面积为24cm2,一个球内切于该正方体,结合正方体和圆的结构特征,我们可以求出球的半径,代入球的体积公式即可求出答案.
(2)求出外接球的直径,即可求该正方体的外接球的体积.
解答 解:(1)∵正方体的全面积为24cm2,
∴正方体的棱长为2cm,
又∵球内切于该正方体,
∴这个球的直径为2cm,
则这个球的半径为1cm,
∴球的体积V=$\frac{4π}{3}$cm3,
(2)∵球外接于该正方体,
∴这个球的直径为2$\sqrt{3}$cm,
则这个球的半径为$\sqrt{3}$cm,
∴球的体积V=$\frac{4π}{3}$×$3\sqrt{3}$=4$\sqrt{3}$πcm3.
点评 本题考查的知识点是球的体积,其中根据正方体和圆的结构特征,求出球的半径,是解答本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11.一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,表为抽样试验的结果:
假设y对x有线性相关关系,求回归直线方程;$\widehat{b}$=$\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)÷\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
16.已知函数f(x)=3x-3|x|,若3tf(2t)-mf(t)≥0对于t∈[-2,-1]恒成立,则实数m范围是( )
| A. | [$\frac{1}{9}$,+∞) | B. | (-∞,$\frac{1}{9}$] | C. | [$\frac{10}{9}$,+∞) | D. | (-∞,$\frac{10}{9}$] |
6.下列各组函数是相等函数的是( )
| A. | y=$\frac{|x|}{x}$与 y=1 | B. | y=$\frac{{x}^{3}+x}{{x}^{2}+1}$与y=x | ||
| C. | y=x与y=($\sqrt{x}$)2 | D. | y=|x|与y=$\left\{\begin{array}{l}{x,x>1}\\{-x,x<1}\end{array}\right.$ |
10.要从已编号(1-60)的60名学生中随机抽取6人,现用系统抽样方法确定所选取的6个同学的编号可能是( )
| A. | 5,10,15,20,25,30 | B. | 2,4,8,16,32,48 | ||
| C. | 1,2,3,4,5,6 | D. | 3,13,23,33,43,53 |
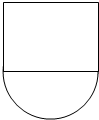 以长为2的铁丝围成上部为矩形,下部为半圆形的框架,如果半圆的直径为2x,求此框架围成图形(如图所示)的面积为y与x的函数关系式y=f(x),并写出它的定义域.
以长为2的铁丝围成上部为矩形,下部为半圆形的框架,如果半圆的直径为2x,求此框架围成图形(如图所示)的面积为y与x的函数关系式y=f(x),并写出它的定义域.