题目内容
【题目】已知两条直线l1：y＝m 和l2：y
（m＞0），直线l1与函数y＝|log2x|的图象从左至右相交于点A，B，直线l2与函数y＝|log2x|的图象从左至右相交于C，D．记线段AC和BD在X轴上的投影长度分别为a 和b．当m变化时，
的最小值为（）
A. 
B. 
C. 
D. 
【答案】D
【解析】
由题意设A，B，C，D各点的横坐标分别为xA，xB，xC，xD，依题意可求得为xA，xB，xC，xD的值，a＝|xA﹣xC|，b＝|xB﹣xD|，下面利用基本不等式可求最小值．
解：设A，B，C，D各点的横坐标分别为xA，xB，xC，xD，
则﹣log2xA＝m，log2xB＝m；﹣log2xC
，log2xD；
∴xA＝2﹣m，xB＝2m，xC
，xD
．
∴a＝|xA﹣xC|，b＝|xB﹣xD|，
∴
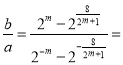2m
又m＞0，∴m
（2m+1）
2
，
当且仅当
，即m
时取“＝”号，
∴
8
，
故选D．
练习册系列答案
阅读快车系列答案
相关题目
【题目】2018年6月14日，世界杯足球赛在俄罗斯拉开帷幕.通过随机调查某小区100名性别不同的居民是否观看世界杯比赛，得到以下列联表：
观看世界杯 | 不观看世界杯 | 总计 | |
男 | 40 | 20 | 60 |
女 | 15 | 25 | 40 |
总计 | 55 | 45 | 100 |
经计算
的观测值
.
附表：
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参照附表，所得结论正确的是（ ）
A. 有
以上的把握认为“该小区居民是否观看世界杯与性别有关”
B. 有以上的把握认为“该小区居民是否观看世界杯与性别无关”
C. 在犯错误的概率不超过0.005的前提下，认为“该小区居民是否观看世界杯与性别有关”
D. 在犯错误的概率不超过0.001的前提下，认为“该小区居民是否观看世界杯与性别无关”
