题目内容
已知二次函数f(x)=ax2+bx+c的导数为f′(x),f′(0)>0,对于任意实数x都有f(x)≥0,则的最小值为( )
A.3 B. C.2 D.
A.3 B. C.2 D.
C
先根据题目的条件建立关于a、b、c的关系式,再结合基本不等式求出最小即可,注意等号成立的条件.
解:∵f(x)=ax2+bx+c
∴f′(x)=2ax+b,f′(0)=b>0
∵对任意实数x都有f(x)≥0
∴a>0,c>0,b2-4ac≤0即4ac/b2≥ 1
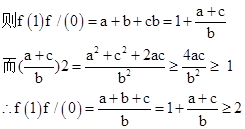
故答案为2

练习册系列答案
相关题目
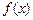 =
=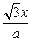 +
+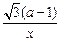 ,a≠0且a≠1.
,a≠0且a≠1.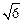 )上单调递减,在(
)上单调递减,在(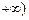 上单调递增,求a的值并写出函数的解析式;
上单调递增,求a的值并写出函数的解析式;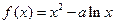 (常数
(常数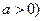 .
.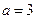 时,求曲线
时,求曲线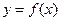 在点
在点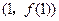 处的切线方程;
处的切线方程;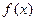 在区间
在区间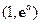 上零点的个数(
上零点的个数(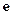 为自然对数的底数).
为自然对数的底数).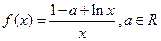 .
.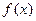 的极值;
的极值;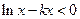 在
在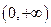 上恒成立,求
上恒成立,求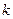 的取值范围;
的取值范围;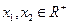 ,且
,且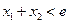 ,求证:
,求证: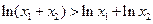 .
.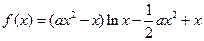 .
.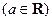 .
.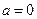 时,求曲线
时,求曲线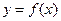 在
在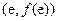 处的切线方程(
处的切线方程(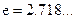 );
);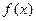 的单调区间.
的单调区间.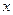 艘的产值函数为
艘的产值函数为 (单位:万元),成本函数为
(单位:万元),成本函数为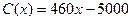 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数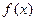 的边际函数
的边际函数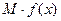 定义为
定义为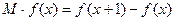 。
。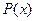 及边际利润函数
及边际利润函数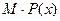 ;(提示:利润=产值-成本)
;(提示:利润=产值-成本)
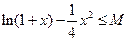 恒成立,则
恒成立,则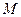 的最小值为 .
的最小值为 .