题目内容
已知函数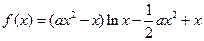 .
.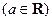 .
.
(I)当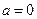 时,求曲线
时,求曲线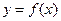 在
在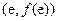 处的切线方程(
处的切线方程(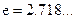 );
);
(II)求函数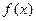 的单调区间.
的单调区间.
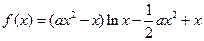 .
.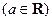 .
.(I)当
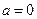 时,求曲线
时,求曲线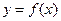 在
在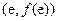 处的切线方程(
处的切线方程(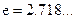 );
);(II)求函数
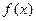 的单调区间.
的单调区间.解:(I)当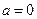 时,
时, ,
,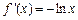 , ………………………2分
, ………………………2分
所以 ,
,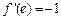 , ………………………4分
, ………………………4分
所以曲线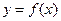 在
在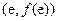 处的切线方程为
处的切线方程为 .………………………5分
.………………………5分
(II)函数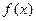 的定义域为
的定义域为
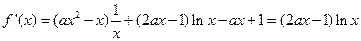 ,…………………………6分
,…………………………6分
①当 时,
时, ,在
,在 上
上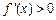 ,在
,在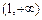 上
上
所以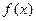 在
在 上单调递增,在
上单调递增,在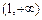 上递减; …………………………8分
上递减; …………………………8分
②当 时,在
时,在 和
和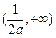 上
上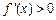 ,在
,在 上
上
所以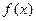 在
在 和
和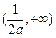 上单调递增,在
上单调递增,在 上递减;………………………10分
上递减;………………………10分
③当 时,在
时,在 上
上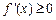 且仅有
且仅有 ,
,
所以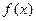 在
在 上单调递增; …………………………12分
上单调递增; …………………………12分
④当 时,在
时,在 和
和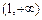 上
上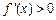 ,在
,在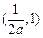 上
上
所以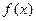 在
在 和
和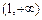 上单调递增,在
上单调递增,在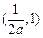 上递减……………………………14分
上递减……………………………14分
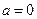 时,
时, ,
,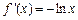 , ………………………2分
, ………………………2分所以
 ,
,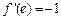 , ………………………4分
, ………………………4分所以曲线
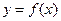 在
在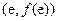 处的切线方程为
处的切线方程为 .………………………5分
.………………………5分(II)函数
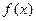 的定义域为
的定义域为
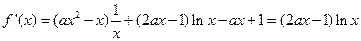 ,…………………………6分
,…………………………6分①当
 时,
时, ,在
,在 上
上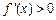 ,在
,在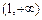 上
上
所以
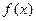 在
在 上单调递增,在
上单调递增,在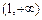 上递减; …………………………8分
上递减; …………………………8分②当
 时,在
时,在 和
和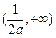 上
上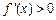 ,在
,在 上
上
所以
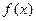 在
在 和
和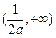 上单调递增,在
上单调递增,在 上递减;………………………10分
上递减;………………………10分③当
 时,在
时,在 上
上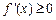 且仅有
且仅有 ,
,所以
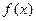 在
在 上单调递增; …………………………12分
上单调递增; …………………………12分④当
 时,在
时,在 和
和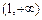 上
上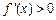 ,在
,在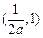 上
上
所以
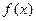 在
在 和
和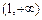 上单调递增,在
上单调递增,在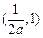 上递减……………………………14分
上递减……………………………14分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
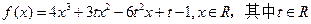 ,
,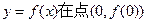 处的切线方程;
处的切线方程; 在区间(0,1)内均存在零点。
在区间(0,1)内均存在零点。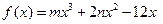 的减区间是
的减区间是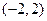 .
.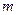 、
、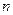 的值;
的值;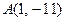 且与曲线
且与曲线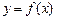 相切的切线方程;
相切的切线方程;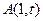 是否存在与曲线
是否存在与曲线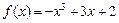 分别在
分别在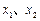 处取得极小值、极大值.
处取得极小值、极大值.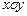 平面上点
平面上点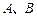 的坐标分别为
的坐标分别为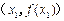 、
、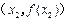 ,该平面上动点
,该平面上动点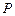 满足
满足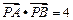 ,点
,点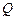 是点
是点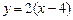 的对称点,.求
的对称点,.求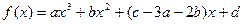 的图像如图所示。
的图像如图所示。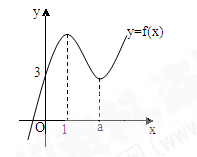
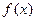 在
在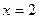 处的切线方程为
处的切线方程为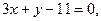 求函数
求函数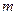 ,使得
,使得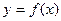 的图像与
的图像与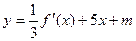
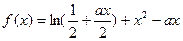
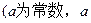 >0)
>0) 的一个极值点,求
的一个极值点,求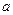 的值;
的值;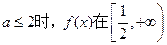 上是增函数;
上是增函数;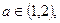 总存在
总存在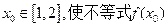 >
>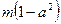 成立,求实数m的取值范围。
成立,求实数m的取值范围。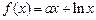
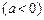 .
.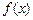 的单调区间;
的单调区间;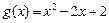 ,若对任意
,若对任意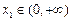 ,均存在
,均存在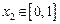 ,使得
,使得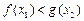 ,求
,求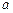 的取值范围.
的取值范围. 的图象过点P( 1,2),且在点P处的切线与直线x-3y=0垂直.
的图象过点P( 1,2),且在点P处的切线与直线x-3y=0垂直.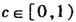 ,试求函数f(x)的单调区间;
,试求函数f(x)的单调区间; ,m),(n,
,m),(n,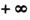 )是f(x)的单调递
)是f(x)的单调递 增区间,试求n-m-2c的范围
增区间,试求n-m-2c的范围