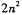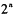题目内容
已知函数f(x)=x2+ln x-1.
(1)求函数f(x)在区间[1,e](e为自然对数的底)上的最大值和最小值;
(2)求证:在区间(1,+∞)上,函数f(x)的图象在函数g(x)=x3的图象的下方
(3)(理)求证:[f′(x)]n-f′(xn)≥2n-2(n∈N*)
(1)求函数f(x)在区间[1,e](e为自然对数的底)上的最大值和最小值;
(2)求证:在区间(1,+∞)上,函数f(x)的图象在函数g(x)=x3的图象的下方
(3)(理)求证:[f′(x)]n-f′(xn)≥2n-2(n∈N*)
(1)∵f′(x)=x+,
当x∈[1,e]时,f′(x)>0.∴函数f(x)在[1,e]上为增函数,
∴f(x)max=f(e)=e2,f(x)min=f(1)=-.
(2)证明:令F(x)=f(x)-g(x)=x2+ln x-1-x3
则F′(x)=x+-2x2=
=.
∵当x>1时F′(x)<0,∴函数F(x)在区间(1,+∞)上为减函数,∴F(x)<F(1)=-1-<0,
即在(1,+∞)上,f(x)<g(x).
∴在区间(1,+∞)上,函数f(x)的图象在函数g(x)=x3的图象的下方.
(3)(理)证明:∵f′(x)=x+,
当n=1时,不等式显然成立;当n≥2时,
∵[f′(x)]n-f′(xn)=n-
=Cxn-2+Cxn-3+…+C,①
[f′(x)]n-f′(xn)=C+C+…+Cxn-2,②
①+②得[f′(x)]n-f′(xn)=
≥C+C+…+C=2n-2(当且仅当x=1时“=”成立).
∴当n≥2时,不等式成立.
综上所述得[f′(x)]n-f′(xn)≥2n-2(n∈N+).
当x∈[1,e]时,f′(x)>0.∴函数f(x)在[1,e]上为增函数,
∴f(x)max=f(e)=e2,f(x)min=f(1)=-.
(2)证明:令F(x)=f(x)-g(x)=x2+ln x-1-x3
则F′(x)=x+-2x2=
=.
∵当x>1时F′(x)<0,∴函数F(x)在区间(1,+∞)上为减函数,∴F(x)<F(1)=-1-<0,
即在(1,+∞)上,f(x)<g(x).
∴在区间(1,+∞)上,函数f(x)的图象在函数g(x)=x3的图象的下方.
(3)(理)证明:∵f′(x)=x+,
当n=1时,不等式显然成立;当n≥2时,
∵[f′(x)]n-f′(xn)=n-
=Cxn-2+Cxn-3+…+C,①
[f′(x)]n-f′(xn)=C+C+…+Cxn-2,②
①+②得[f′(x)]n-f′(xn)=
≥C+C+…+C=2n-2(当且仅当x=1时“=”成立).
∴当n≥2时,不等式成立.
综上所述得[f′(x)]n-f′(xn)≥2n-2(n∈N+).
略

练习册系列答案
相关题目
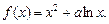
 时,求函数
时,求函数 的单调区间;
的单调区间; 在
在 是单调函数,求实数
是单调函数,求实数 的取值范围.
的取值范围.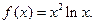
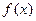 的单调区间;
的单调区间;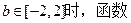
 ,在(1,2)上为单调递
,在(1,2)上为单调递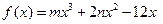 的减区间是
的减区间是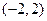 .
.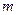 、
、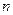 的值;
的值;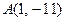 且与曲线
且与曲线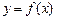 相切的切线方程;
相切的切线方程;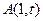 是否存在与曲线
是否存在与曲线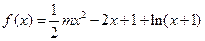
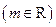
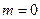 时,求函数
时,求函数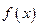 的最大值;
的最大值; 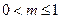 时,曲线
时,曲线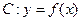 在点
在点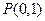 处的切线
处的切线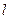 与
与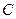 有且只有一个公共
有且只有一个公共 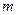 的值.
的值.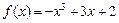 分别在
分别在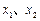 处取得极小值、极大值.
处取得极小值、极大值.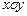 平面上点
平面上点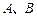 的坐标分别为
的坐标分别为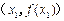 、
、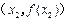 ,该平面上动点
,该平面上动点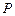 满足
满足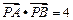 ,点
,点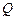 是点
是点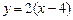 的对称点,.求
的对称点,.求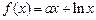
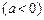 .
.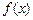 的单调区间;
的单调区间;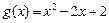 ,若对任意
,若对任意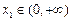 ,均存在
,均存在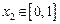 ,使得
,使得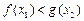 ,求
,求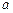 的取值范围.
的取值范围.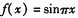 是[0,1]上的函数,且定义
是[0,1]上的函数,且定义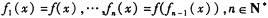 ,则满足
,则满足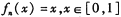 的x的个数是
的x的个数是