题目内容
【题目】已知函数f(x)=x2-ax+ln(x+1)(a∈R).
(1)当a=2时,求函数f(x)的极值点;
(2)若函数f(x)在区间(0,1)上恒有f′(x)>x,求实数a的取值范围;
(3)已知a<1,c1>0,且cn+1=f′(cn)(n=1,2,…),证明数列{cn}是单调递增数列.
【答案】解析
【解析】(1)当a=2时,f(x)=x2-2x+ln(x+1),
f′(x)=2x-2+![]() =
=![]() .
.
令f′(x)=0,得x=±![]() .
.
当x∈![]() 时,f′(x)>0,f(x)单调递增;
时,f′(x)>0,f(x)单调递增;
当x∈![]() 时,f′(x)<0,f(x)单调递减.
时,f′(x)<0,f(x)单调递减.
当x∈![]() 时,f′(x)>0,f(x)单调递增.
时,f′(x)>0,f(x)单调递增.
所以函数f(x)的极大值点为x=-![]() ,极小值点为x=
,极小值点为x=![]() .
.
(2)因为f′(x)=2x-a+![]() ,
,
由f′(x)>x,得2x-a+![]() >x,
>x,
所以由题意知,a<x+![]() (0<x<1)恒成立.
(0<x<1)恒成立.
又x+![]() =x+1+
=x+1+![]() -1≥1,当且仅当x+1=
-1≥1,当且仅当x+1=![]() ,即x=0时等号成立.
,即x=0时等号成立.
所以a≤1.
故所求实数a的取值范围为(-∞,1].
(3)证明:①当n=1时,c2=f′(c1)=2c1-a+![]() .
.
因为c1>0,所以c1+1>1,又a<1,
所以c2-c1=c1-a+![]() =c1+1+
=c1+1+![]() -(a+1)>2-(a+1)=1-a>0,
-(a+1)>2-(a+1)=1-a>0,
所以c2>c1,即当n=1时结论成立.
②假设当n=k(k∈N*,k≥1)时结论成立,即ck+1>ck>0,
当n=k+1时,
ck+2-ck+1=ck+1-a+![]() =ck+1+1+
=ck+1+1+![]() -(a+1)>2-(a+1)=1-a>0.
-(a+1)>2-(a+1)=1-a>0.
所以ck+2>ck+1,即当n=k+1时结论成立.
由①②知数列{cn}是单调递增数列.

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试,分数分布如表:
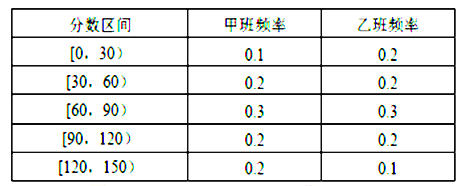
(1)若成绩120分以上(含120分)为优秀,求从乙班参加测试的90分以上(含90分)的同学中,随机任取2名同学,恰有1人为优秀的概率;
(2)根据以上数据完成下面的![]() 列联表:在犯错概率小于
列联表:在犯错概率小于![]() 的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?
的前提下,你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系?

| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
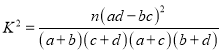 ,其中
,其中![]() .
.