题目内容
(选修4-4:坐标系与参数方程)
已知椭圆的长轴长为6,焦距F1F2=4 ,过椭圆左焦点F1作一直线,交椭圆于两点M、N,设∠F2F1M=α(0≤α<π),当α为何值时,MN与椭圆短轴长相等?(用极坐标或参数方程方程求解)
,过椭圆左焦点F1作一直线,交椭圆于两点M、N,设∠F2F1M=α(0≤α<π),当α为何值时,MN与椭圆短轴长相等?(用极坐标或参数方程方程求解)
解:以椭圆焦点F1为极点,
以F1为起点并过F2的射线为极轴建立极坐标系
由已知条件可知椭圆长半轴a=3,
半焦距c= ,短半轴b=1,
,短半轴b=1,
离心率e= ,中心到准线距离=
,中心到准线距离=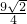 ,
,
焦点到准线距离p= .
.
椭圆的极坐标方程为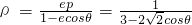
∴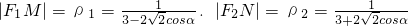 ,
,
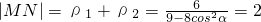 .
.
解得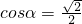 .
.
∴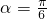 或
或 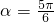 .
.
以上解方程过程中的每一步都是可逆的,
所以当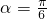 或
或 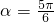 时,|MN|等于短轴的长.
时,|MN|等于短轴的长.
分析:以椭圆焦点F1为极点,以F1为起点并过F2的射线为极轴建立极坐标系,由已知条件可知椭圆的极坐标方程为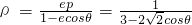 ∴
∴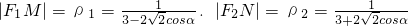 ,
,
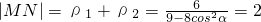 .据此能够求出α的值.
.据此能够求出α的值.
点评:本小题主要考查椭圆的简单性质、椭圆的极坐标方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
以F1为起点并过F2的射线为极轴建立极坐标系
由已知条件可知椭圆长半轴a=3,
半焦距c=
 ,短半轴b=1,
,短半轴b=1,离心率e=
 ,中心到准线距离=
,中心到准线距离=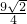 ,
,焦点到准线距离p=
 .
.椭圆的极坐标方程为
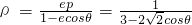
∴
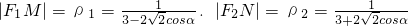 ,
,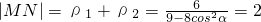 .
.解得
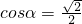 .
.∴
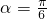 或
或 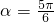 .
.以上解方程过程中的每一步都是可逆的,
所以当
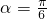 或
或 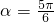 时,|MN|等于短轴的长.
时,|MN|等于短轴的长.分析:以椭圆焦点F1为极点,以F1为起点并过F2的射线为极轴建立极坐标系,由已知条件可知椭圆的极坐标方程为
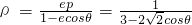 ∴
∴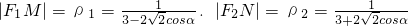 ,
,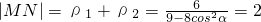 .据此能够求出α的值.
.据此能够求出α的值.点评:本小题主要考查椭圆的简单性质、椭圆的极坐标方程等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲