题目内容
 A.选修4-1:几何证明选讲
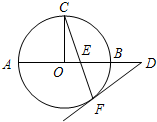
A.选修4-1:几何证明选讲如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC
交于点D.求证:ED2=EB•EC.
B.选修4-2:矩阵与变换
求矩阵M=
|
C.选修4-4:坐标系与参数方程
在以O为极点的极坐标系中,直线l与曲线C的极坐标方程分别是ρcos(θ+
| π |
| 4 |
3
| ||
| 2 |
D.选修4-5:不等式选讲
对于实数x,y,若|x-1|≤1,|y-2|≤1,求|x-y+1|的最大值.
分析:A.由弦切角定理,得∠CAE=∠CBA,结合AD是∠BAC的平分线和三角形的外角定理,得EA=ED.最后根据切割线定理结合等量代换,得ED2=EB•EC.
B.根据公式列出f(λ)=0,可解出两个特征值λ1=7,λ2=-2.再结合条件,列出特征向量满足的方程组,将解出的x、y值变成列矩阵,即可得到属于这两个特征值特征向量.
C.将直线l与曲线C的极坐标方程化成直角坐标方程,联解可得交点分别为A(1,-2)和B(9,6),最后用平面内两点之间的距离公式,可算出线段AB的长.
D.以x-1和y-2为基本量,利用绝对值三角不等式可得|x-y+1|≤|x-1|+|y-2|,结合已知条件不难得到|x-y+1|的最大值.
B.根据公式列出f(λ)=0,可解出两个特征值λ1=7,λ2=-2.再结合条件,列出特征向量满足的方程组,将解出的x、y值变成列矩阵,即可得到属于这两个特征值特征向量.
C.将直线l与曲线C的极坐标方程化成直角坐标方程,联解可得交点分别为A(1,-2)和B(9,6),最后用平面内两点之间的距离公式,可算出线段AB的长.
D.以x-1和y-2为基本量,利用绝对值三角不等式可得|x-y+1|≤|x-1|+|y-2|,结合已知条件不难得到|x-y+1|的最大值.
解答:解:A.∵EA是圆的切线,AC为过切点A的弦,∴∠CAE=∠CBA.
又∵AD是∠BAC的平分线,∴∠BAD=∠CAD
∴∠DAE=∠DAC+∠EAC=∠BAD+∠CBA=∠ADE
∴△EAD是等腰三角形,得EA=ED.
又∵EA2=EC•EB,∴ED2=EB•EC.
B.由题意,得f(λ)=(λ+1)(λ-6)-8=λ2-5λ-14=(λ-7)(λ+2)
由f(λ)=0,得λ1=7,λ2=-2
根据
,可得
,所以属于λ1=7的一个特征向量为
根据
,可得
,所以属于λ2=-2的一个特征向量为
C、ρcos(θ+
)=
化简,得ρcosθ-ρsinθ=3
∵ρcosθ=x,ρsinθ=y,∴直线l的直角坐标方程为x-y-3=0
同理,抛物线ρsin2θ=4cosθ化成直角坐标方程y2=4x
将直线方程与抛物线方程联解,得
或
∴直线与抛物线交于点A(1,-2)和B(9,6)
由两点的距离公式,得线段AB的长为
=8
D、∵|x-1|≤1,|y-2|≤1,
∴|x-y+1|=|(x-1)-(y-2)|≤|x-1|+|y-2|≤1+1=2,
故|x-y+1|的最大值为2,当且仅当 x=2,y=3,或x=0,y=1时取等号.
又∵AD是∠BAC的平分线,∴∠BAD=∠CAD
∴∠DAE=∠DAC+∠EAC=∠BAD+∠CBA=∠ADE
∴△EAD是等腰三角形,得EA=ED.
又∵EA2=EC•EB,∴ED2=EB•EC.
B.由题意,得f(λ)=(λ+1)(λ-6)-8=λ2-5λ-14=(λ-7)(λ+2)
由f(λ)=0,得λ1=7,λ2=-2
根据
|
|
|
根据
|
|
|
C、ρcos(θ+
| π |
| 4 |
3
| ||
| 2 |
∵ρcosθ=x,ρsinθ=y,∴直线l的直角坐标方程为x-y-3=0
同理,抛物线ρsin2θ=4cosθ化成直角坐标方程y2=4x
将直线方程与抛物线方程联解,得
|
|
∴直线与抛物线交于点A(1,-2)和B(9,6)
由两点的距离公式,得线段AB的长为
| (1-9)2+(-2-6)2 |
| 2 |
D、∵|x-1|≤1,|y-2|≤1,
∴|x-y+1|=|(x-1)-(y-2)|≤|x-1|+|y-2|≤1+1=2,
故|x-y+1|的最大值为2,当且仅当 x=2,y=3,或x=0,y=1时取等号.
点评:本题主要考查了简单曲线的极坐标方程、特征值与特征向量的计算、与圆有关的比例线段和绝对值三角不等式等知识,考查了同学们对理科选修知识的掌握,属于中档题.

练习册系列答案
相关题目
 A(选修4-1:几何证明选讲)
A(选修4-1:几何证明选讲) 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤. A)选修4-1:几何证明选讲
A)选修4-1:几何证明选讲 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分. 从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)