题目内容
本题(1)、(2)、(3)三个选答题,每小题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分.
(1)选修4-2:矩阵与变换
已知矩阵A=
,若矩阵A属于特征值6的一个特征向量为
=
,属于特征值1的一个特征向量为
=
&-2;
(Ⅰ)求矩阵A;
(Ⅱ)判断矩阵A是否可逆,若可逆求出其逆矩阵A-1.
(2)选修4-4:坐标系与参数方程
已知直线的极坐标方程为ρsin(θ+
)=
,圆M的参数方程为
(其中θ为参数).
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆M上的点到直线的距离的最小值.
(3)选修4-5:不等式选讲,设函数f(x)=|x-1|+|x-a|;
(Ⅰ)若a=-1,解不等式f(x)≥3;
(Ⅱ)如果关于x的不等式f(x)≤2有解,求a的取值范围.
(1)选修4-2:矩阵与变换
已知矩阵A=
|
| α |
|
| β |
|
(Ⅰ)求矩阵A;
(Ⅱ)判断矩阵A是否可逆,若可逆求出其逆矩阵A-1.
(2)选修4-4:坐标系与参数方程
已知直线的极坐标方程为ρsin(θ+
| π |
| 4 |
| ||
| 2 |
|
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆M上的点到直线的距离的最小值.
(3)选修4-5:不等式选讲,设函数f(x)=|x-1|+|x-a|;
(Ⅰ)若a=-1,解不等式f(x)≥3;
(Ⅱ)如果关于x的不等式f(x)≤2有解,求a的取值范围.
分析:(1)(Ⅰ)利用矩阵属于特征值的一个特征向量的定义,我们可以建立方程,从而可以求出c=2,d=4,即可得到矩阵A;
(Ⅱ)根据
=6≠0,可知矩阵A可逆,,从而可求出A-1=
(2)(Ⅰ)先利用和角的三角函数展开,再利用极坐标与直角坐标的互化公式可以求出直线的直角坐标方程;
(Ⅱ)利用圆M的普通方程为:x2+(y+2)2=4,再根据圆心M(0,-2)到直线x+y-1=0的距离公式,我们可以求出圆M上的点到直线的距离的最小值;
(3)(Ⅰ)当a=-1时,f(x)=|x-1|+|x+1|.由f(x)≥3,得,|x-1|+|x+1|≥3,分类讨论,我们可以求出不等式的解集;
(Ⅱ)因为关于x的不等式f(x)≤2有解,所以,f(x)min≤2,从而我们可以得到|a-1|≤2,即可求出a的取值范围.
(Ⅱ)根据
|
|
(2)(Ⅰ)先利用和角的三角函数展开,再利用极坐标与直角坐标的互化公式可以求出直线的直角坐标方程;
(Ⅱ)利用圆M的普通方程为:x2+(y+2)2=4,再根据圆心M(0,-2)到直线x+y-1=0的距离公式,我们可以求出圆M上的点到直线的距离的最小值;
(3)(Ⅰ)当a=-1时,f(x)=|x-1|+|x+1|.由f(x)≥3,得,|x-1|+|x+1|≥3,分类讨论,我们可以求出不等式的解集;
(Ⅱ)因为关于x的不等式f(x)≤2有解,所以,f(x)min≤2,从而我们可以得到|a-1|≤2,即可求出a的取值范围.
解答:(1)解:(Ⅰ)∵矩阵A属于特征值6的一个特征向量为
=
,∴A
=6
∴
=6
,得c+d=6①---------------(2分)
同理
=
,得,3c-2d=-2②----------------(3分)
由①②联立,解得,c=2,d=4;∴A=
…(4分)
(Ⅱ)∵
=6≠0,∴矩阵A可逆,…(5分)
∴A-1=
…(7分)
(2)(Ⅰ)∵ρsin(θ+
)=
,∴
(ρsinθ+ρcosθ)=
,
∴ρsinθ+ρcosθ=1.----------------(2分)
所以,该直线的直角坐标方程为:x+y-1=0.----------------(3分)
(Ⅱ)圆M的普通方程为:x2+(y+2)2=4----------------(4分)
圆心M(0,-2)到直线x+y-1=0的距离d=
=
.---------------(5分)
所以,圆M上的点到直线的距离的最小值为
-2.----------------(7分)
(3)(Ⅰ)当a=-1时,f(x)=|x-1|+|x+1|.
由f(x)≥3,得,|x-1|+|x+1|≥3.
①当x≤-1时,不等式化为1-x-1-x≥3,即x≤-
.所以,原不等式的解为x≤-
.…(1分)
②当-1<x<1时,不等式化为1-x+1+x≥3,即2≥3.所以,原不等式无解.…(2分)
③当x≥1时,不等式化为-1+x+1+x≥3,即x≥
.所以,原不等式的解为x≥
.…(3分)
综上,原不等式的解为(-∞,-
]∪[
,+∞).…(4分)
(Ⅱ)因为关于x的不等式f(x)≤2有解,所以,f(x)min≤2.…(5分)
因为|x-1|+|x-a|表示数轴上的点到x=1与x=a两点的距离之和,
所以,f(x)min=|a-1|.…(6分)
∴|a-1|≤2,解得,-1≤a≤3.
所以,a的取值范围为[-1,3].…(7分)
| α |
|
| α |
| α |
∴
|
|
|
同理
|
|
|
由①②联立,解得,c=2,d=4;∴A=
|
(Ⅱ)∵
|
∴A-1=
|
(2)(Ⅰ)∵ρsin(θ+
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴ρsinθ+ρcosθ=1.----------------(2分)
所以,该直线的直角坐标方程为:x+y-1=0.----------------(3分)
(Ⅱ)圆M的普通方程为:x2+(y+2)2=4----------------(4分)
圆心M(0,-2)到直线x+y-1=0的距离d=
| |0-2-1| | ||
|
3
| ||
| 2 |
所以,圆M上的点到直线的距离的最小值为
3
| ||
| 2 |
(3)(Ⅰ)当a=-1时,f(x)=|x-1|+|x+1|.
由f(x)≥3,得,|x-1|+|x+1|≥3.
①当x≤-1时,不等式化为1-x-1-x≥3,即x≤-
| 3 |
| 2 |
| 3 |
| 2 |
②当-1<x<1时,不等式化为1-x+1+x≥3,即2≥3.所以,原不等式无解.…(2分)
③当x≥1时,不等式化为-1+x+1+x≥3,即x≥
| 3 |
| 2 |
| 3 |
| 2 |
综上,原不等式的解为(-∞,-
| 3 |
| 2 |
| 3 |
| 2 |
(Ⅱ)因为关于x的不等式f(x)≤2有解,所以,f(x)min≤2.…(5分)
因为|x-1|+|x-a|表示数轴上的点到x=1与x=a两点的距离之和,
所以,f(x)min=|a-1|.…(6分)
∴|a-1|≤2,解得,-1≤a≤3.
所以,a的取值范围为[-1,3].…(7分)
点评:本题是选做题,考查矩阵,坐标系与参数方程,考查不等式,熟悉各个知识点,熟练运用公式是我们解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,若
,若 所对应的变换
所对应的变换 把直线
把直线 变换为自身,求实数
变换为自身,求实数 ,并求
,并求 的逆矩阵。
的逆矩阵。 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: 。
。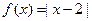
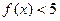 ;
; ,不等式
,不等式 成立.
成立.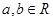 ,若
,若 所对应的变换
所对应的变换 把直线
把直线 变换为自身,求实数
变换为自身,求实数 ,并求
,并求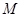 的逆矩阵。
的逆矩阵。 的参数方程:
的参数方程: (
( 为参数)和圆
为参数)和圆 的极坐标方程:
的极坐标方程: 。
。
 ;
; ,不等式
,不等式 成立.
成立.