题目内容
(2013•广东模拟)(选修4-4:坐标系与参数方程选讲)
在直角坐标系xOy中,以原点O为极点,以x轴非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C参数方程为
(θ为参数),直线l的极坐标方程为ρcos(θ-
)=2
.则曲线C上的点到直线l的最大距离是
在直角坐标系xOy中,以原点O为极点,以x轴非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C参数方程为
|
| π |
| 4 |
| 2 |
3
| 2 |
3
.| 2 |
分析:先把直线l的极坐标方程化为直角坐标方程,然后在曲线C上任取一点P(
cosθ,sinθ),由点到直线的距离公式可表示出点P到直线l的距离d,利用三角函数公式即可求得d的最大值.
| 3 |
解答:解:由ρcos(θ-
)=2
,得ρ(cosθ+sinθ)=4,
∴l:x+y-4=0.
在C:
上任取一点P(
cosθ,sinθ),
则点P到直线l的距离为d=
=
≤3
.
∴当sin(θ+
)=-1时,dmax=3
.
故答案为:3
.
| π |
| 4 |
| 2 |
∴l:x+y-4=0.
在C:
|
| 3 |
则点P到直线l的距离为d=
|
| ||
|
|2sin(θ+
| ||
|
| 2 |
∴当sin(θ+
| π |
| 3 |
| 2 |
故答案为:3
| 2 |
点评:本题考查参数方程、极坐标方程、点到直线的距离公式,考查学生分析解决问题的能力,属中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
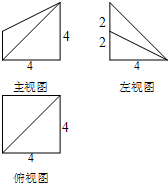 (2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为
(2013•广东模拟)一几何体的三视图如图所示,则这个几何体的体积为