题目内容
【题目】小王大学毕业后,决定利用所学专业进行自主创业.经过市场调查,生产某小型电子产品需投入年固定成本3万元,每生产x万件,该产品需另投入流动成本![]() 万元.在年产量不足8万件时,
万元.在年产量不足8万件时,![]() ,在年产量不小于8万件时,
,在年产量不小于8万件时,![]() 每件产品的售价为5元.通过市场分析,小王生产的商品能当年全部售完.
每件产品的售价为5元.通过市场分析,小王生产的商品能当年全部售完.
(1)写出年利润![]() 单位:万元
单位:万元![]() 关于年产量
关于年产量![]() 单位:万件
单位:万件![]() 的函数解析式.
的函数解析式.
(2)年产量为多少万件时,小王在这一商品的生产中所获利润最大?最大利润是多少?
![]() 注:年利润
注:年利润![]() 年销售收入
年销售收入![]() 固定成本
固定成本![]() 流动成本
流动成本![]()
【答案】(1)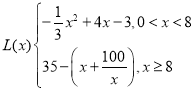 .(2)产量为10万件时,最大利润为15万元.
.(2)产量为10万件时,最大利润为15万元.
【解析】
(1)根据年利润![]() 年销售收入
年销售收入![]() 固定成本
固定成本![]() 流动成本,分
流动成本,分![]() 和
和![]() 两种情况分别列出
两种情况分别列出![]() 与
与![]() 的分段函数关系式;
的分段函数关系式;
(2)当![]() 时,利用配方法求二次函数
时,利用配方法求二次函数![]() 的最大值,当
的最大值,当![]() 时,利用基本不等式求出
时,利用基本不等式求出![]() 的最大值,最后取较大的
的最大值,最后取较大的![]() 的值即可.
的值即可.
(1)因为每件商品售价为5元,则x万件商品销售收入为5x万元.
依题意得,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
所以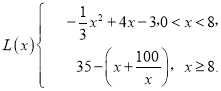
(2)当![]() 时,
时,![]() ,
,
此时,当![]() 时,
时,![]() 取得最大值
取得最大值![]() 万元
万元![]() ,
,
当![]() 时,
时,![]() ,
,
此时,当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最大值15万元,
取得最大值15万元,
因为![]() ,所以,当年产量为10万件时,小王在这一商品的生产中所获利润最大,最大利润为15万元.
,所以,当年产量为10万件时,小王在这一商品的生产中所获利润最大,最大利润为15万元.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】某校100名学生期中考试语文成绩的频率分布直方图如图4所示,其中成绩分组区间是: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示,求数学成绩在
之比如下表所示,求数学成绩在![]() 之外的人数.
之外的人数.
分数段 |
|
|
|
|
X:y | 1:1 | 2:1 | 3:4 | 4:5 |
【题目】总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取6个个体,选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为( )
7816 6572 0802 6314 0702 4369 9728 0198 |
3204 9234 4935 8200 3623 4869 6938 7481 |
A.07B.04C.02D.01


