题目内容
【题目】已知![]() .
.
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)若![]() 有三个零点时,求
有三个零点时,求![]() 的范围.
的范围.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)令![]() ,
,![]() ,
,![]() ,利用导数可得
,利用导数可得![]() 在
在![]() 上单调递减,
上单调递减,![]() ,从而可得结论; (2)
,从而可得结论; (2)![]() 有三个零点等价于
有三个零点等价于![]() 有三个零点,当
有三个零点,当![]() 时,当
时,当![]() 时,可得
时,可得![]() 是单调函数,至多有一个零点,不符合题意,当
是单调函数,至多有一个零点,不符合题意,当![]() 时,利用导数研究函数的单调性,根据单调性,结合函数图象可得
时,利用导数研究函数的单调性,根据单调性,结合函数图象可得![]() 的范围是
的范围是![]() .
.
详解:(1)证明: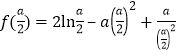 ,
,
令![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,
所以原命题成立.
(2)由![]()
![]() 有三个零点可得
有三个零点可得
![]() 有三个零点,
有三个零点,
![]() ,
,
①当![]() 时,
时,![]() 恒成立,可得
恒成立,可得![]() 至多有一个零点,不符合题意;
至多有一个零点,不符合题意;
②当![]() 时,
时,![]() 恒成立,可得
恒成立,可得![]() 至多有一个零点,不符合题意;
至多有一个零点,不符合题意;
③当![]() 时,记
时,记![]() 得两个零点为
得两个零点为![]() ,
,![]() ,不妨设
,不妨设![]() ,且
,且![]() ,
,
![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;![]() 时
时![]() ,
,
观察可得![]() ,且
,且![]() ,
,
当![]() 时,
时,![]() ;
;![]() 单调递增,
单调递增,
所以有![]() ,即
,即![]() ,
,
![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() 时
时![]() ,
,![]() 单调递减,
单调递减,
由(1)知,![]() ,且
,且![]() ,所以
,所以![]() 在
在![]() 上有一个零点,
上有一个零点,
由![]() ,且
,且![]() ,所以
,所以![]() 在
在![]() 上有一个零点,
上有一个零点,
综上可知![]() 有三个零点,
有三个零点,
即![]() 有三个零点,
有三个零点,
所求![]() 的范围是
的范围是![]() .
.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了![]() 人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
(1)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“月收入以
的把握认为“月收入以![]() 元为分界点对“楼市限购令”的态度有差异;
元为分界点对“楼市限购令”的态度有差异;
月收入不低于 | 月收入低于 | 合计 | |
赞成 |
|
| ______________ |
不赞成 |
|
| ______________ |
合计 | ______________ | ______________ | ______________ |
(2)若对在![]() 、
、![]() 的被调查者中各随机选取两人进行追踪调查,记选中的
的被调查者中各随机选取两人进行追踪调查,记选中的![]() 人中不赞成“楼市限购令”的人数为
人中不赞成“楼市限购令”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: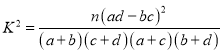 ,其中
,其中![]() .
.
参考值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|




