题目内容
【题目】设函数
（a>0且a≠1）是奇函数．
（1）求常数k的值；
（2）若已知f（1）=
，且函数
在区间[1，+∞]）上的最小值为—2，求实数m的值．
【答案】（1）
；（2）
．
【解析】
试题（1）函数
的定义域为R，∵函数（a>0且a≠1）是奇函数
∴f（0）=k－1=0，∴k=1．
（2）∵f（1）=
，∴
=，解得a=3或
∵a>0且a≠1，∴a=3
g（x）=32x+3-2x－2m（3x－3-x）= （3x－3-x）2－2m（3x－3-x）+2 （x≥1）
令3x－3-x=t （t≥），则y=t2－2mt+2=（t—m）2—m2+2）
当m≥时，
=—m2+2=－2，解得m=2或m=-2，舍去
当m<时，= （）2－2m×+2=－2，解得m=
∴m=．
试题解析：（1）函数的定义域为R
∵函数（a>0且a≠1）是奇函数
∴f（0）=k－1=0
∴k=1
（2）∵f（1）=
∴=，解得a=3或
∵a>0且a≠1
∴a=3
g（x）=32x+3-2x－2m（3x－3-x）= （3x－3-x）2－2m（3x－3-x）+2 （x≥1）
令3x－3-x=t （t≥）
则y=t2－2mt+2=（t—m）2—m2+2
当m≥时，=—m2+2=－2，解得m=2或m=-2，舍去
当m<时，= （）2－2m×+2=－2，解得m=
∴m=
【题目】第一次大考后，某校对甲、乙两个文科班的数学考试成绩进行分析，规定：大于或等于
分为优秀，分以下为非优秀，统计成绩后，得到如下
列联表，且已知在甲、乙两个文科班全部
人中随机抽取
人为优秀的概率为
.
（I）请完成列联表：
优秀 | 非优秀 | 合计 | |
甲班 |
| ||
乙班 |
| ||
合计 |
|
(Ⅱ)根据列联表的数据能否在犯错误的概率不超过
的前提下认为成绩与班级有关系？
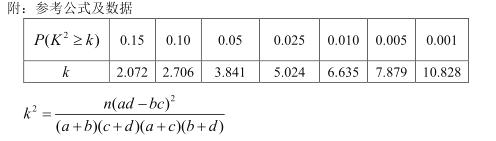
参考公式和临界值表：
，其中
．
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】共享单车已成为一种时髦的新型环保交通工具，某共享单车公司为了拓展市场，对
两个品牌的共享单车在编号分别为
的五个城市的用户人数（单位：十万）进行统计，得到数据如下：
城市 品牌 | 1 | 2 | 3 | 4 | 5 |
A品牌 | 3 | 4 | 12 | 6 | 8 |
B品牌 | 4 | 3 | 7 | 9 | 5 |
（Ⅰ）若共享单车用户人数超过50万的城市称为“优城”，否则称为“非优城”，据此判断能否有85%的把握认为“优城”和共享单车品牌有关？
（Ⅱ）若不考虑其它因素，为了拓展市场，对A品牌要从这五个城市选择三个城市进行宣传，
（ⅰ）求城市2被选中的概率；
（ⅱ）求在城市2被选中的条件下城市3也被选中的概率．
