题目内容
【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了![]() 人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
(1)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“月收入以
的把握认为“月收入以![]() 元为分界点对“楼市限购令”的态度有差异;
元为分界点对“楼市限购令”的态度有差异;
月收入不低于 | 月收入低于 | 合计 | |
赞成 |
|
| ______________ |
不赞成 |
|
| ______________ |
合计 | ______________ | ______________ | ______________ |
(2)若对在![]() 、
、![]() 的被调查者中各随机选取两人进行追踪调查,记选中的
的被调查者中各随机选取两人进行追踪调查,记选中的![]() 人中不赞成“楼市限购令”的人数为
人中不赞成“楼市限购令”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: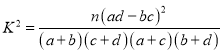 ,其中
,其中![]() .
.
参考值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)列联表见解析,没有![]() 的把握认为月收入以
的把握认为月收入以![]() 元为分界点对“楼市限购令”的态度有差异 ;(2)
元为分界点对“楼市限购令”的态度有差异 ;(2)![]() ,分布列见解析.
,分布列见解析.
【解析】
(1)根据题干表格中的数据补充![]() 列联表,并计算出
列联表,并计算出![]() 的观测值,将观测值与
的观测值,将观测值与![]() 作大小比较,于此可对题中结论进行判断;
作大小比较,于此可对题中结论进行判断;
(2)由题意得出随机变量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() 、
、![]() ,然后利用超几何分布概率公式计算出随机变量
,然后利用超几何分布概率公式计算出随机变量![]() 在相应取值时的概率,可得出随机变量
在相应取值时的概率,可得出随机变量![]() 的分布列,并计算出该随机变量
的分布列,并计算出该随机变量![]() 的数学期望.
的数学期望.
(1)![]() 列联表:
列联表:
月收入不低于 | 月收入低于 | 合计 | |
赞成 |
|
| ____ |
不赞成 |
|
| ______ |
合计 | _______ | ________ | _____ |
![]()
则没有![]() 的把握认为月收入以
的把握认为月收入以![]() 元为分界点对“楼市限购令”的态度有差异;
元为分界点对“楼市限购令”的态度有差异;
(2)![]() 的所有可能取值有:
的所有可能取值有:![]() 、
、![]() 、
、![]() 、
、![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
则![]() 的分布列如下表:
的分布列如下表:
|
|
|
|
|
|
|
|
|
|
则![]() 的期望值是:
的期望值是:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】已知某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组[50,55),第二组[55,60),…,第五组[70,75],按上述分组方法得到的频率分布直方图如图所示.因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若前两组的学生中体育生有8名.
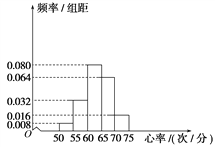
(1)根据频率分布直方图及题设数据完成下列2×2列联表.
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计50 |
(2)根据(1)中表格数据计算可知,________(填“有”或“没有”)99.5%的把握认为“心率小于60次/分与常年进行系统的身体锻炼有关”.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |