题目内容
已知函数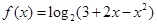
.
(1) 求函数
的定义域;
(2) 求证在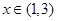
上是减函数;
(3) 求函数的值域.
(1) 的定义域是
(2) 设
, 则
,
, 
, 
,
.
在
上是减函数.
解析
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
已知函数 .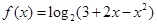
(1) 求函数的定义域;
(2) 求证在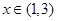上是减函数;
(3) 求函数的值域.
(1) 的定义域是
(2) 设, 则,, , ,.在上是减函数.
解析
名校课堂系列答案
，求函数
=
的最大值与最小值．
.
为何实数
总是为增函数；
上的单调性，并证明你的结论；
}，B=[0,1]， 试判断A与B的关系；
的定义域为
，且满足条件：
，②
③当
的值
的x的取值范围。
，（
且
）。
，令
，试判断函数
在
上的单调性并证明你的结论；
且
的定义域和值域都是
的最大值；
对
恒成立，求实数
的取值范围； 
，
时，
时，
，求
的取值范围。