题目内容
(本题满分14分)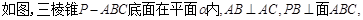
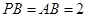 ,
,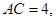
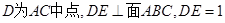 ,P、E在
,P、E在 同侧,连接PE、AE.
同侧,连接PE、AE.
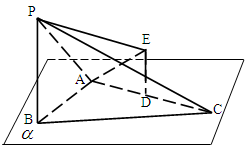
 求证:BC//面APE;
求证:BC//面APE;
 设F是
设F是 内一点,且
内一点,且 ,求直线EF与面APF所成角的大小
,求直线EF与面APF所成角的大小
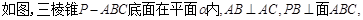
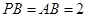 ,
,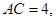
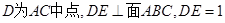 ,P、E在
,P、E在 同侧,连接PE、AE.
同侧,连接PE、AE.
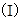 求证:BC//面APE;
求证:BC//面APE; 设F是
设F是 内一点,且
内一点,且 ,求直线EF与面APF所成角的大小
,求直线EF与面APF所成角的大小 (I)见解析;(II)直线EF与平面APF所成角大小为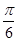 。
。
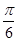 。
。本试题主要是考查了线面平行的判定和线面角的求解的综合运用。
(1)根据线面平行的判定定理,只要证明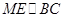 是解决的关键一步。
是解决的关键一步。
(2)分别以AB、AC为x、y轴,过A与面ABC垂直的直线为Z
轴建立空间直角坐标系,然后表示直线的方向向量与平面的法向量,进而得到线面角的大小的求解。
解:
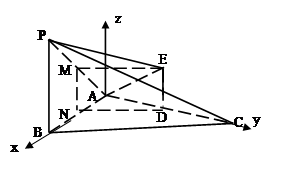
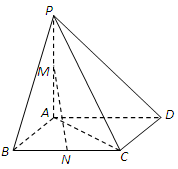
(I)设AP中点为M,AB中点为N,连接EM、DN,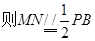 ,
,

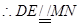 ,
,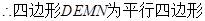 ,
,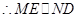 ,……..3分
,……..3分
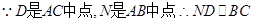 ,由公理4得
,由公理4得
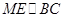 ,
,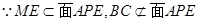
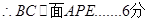
(II)分别以AB、AC为x、y轴,过A与面ABC垂直的直线为Z
轴建立空间直角坐标系…….7分
则B(2,0,0)、C(0,4,0)、P(2,0,2)、
E(0,2,1)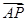 =(2,0,2),
=(2,0,2), =(0,2,1),设F(a,b,0),
=(0,2,1),设F(a,b,0),
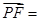 (a-2,b,-2),
(a-2,b,-2),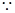 PF
PF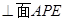 ,
,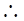
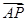
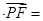 0,得a=4,同理
0,得a=4,同理
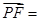 0,得b=1
0,得b=1
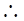 F(4,1,0),…… .9分
F(4,1,0),…… .9分
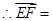 =(4,-1,-1),
=(4,-1,-1),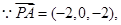
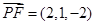
设平面APF法向量为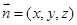 ,由
,由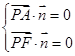 ,得
,得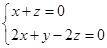 取一组解
取一组解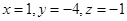 ,
,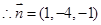 ,……11分
,……11分
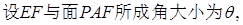
 |cos
|cos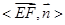 |=
|=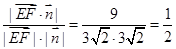 ,
, ,
,  ,直线EF与平面APF所成角大小为
,直线EF与平面APF所成角大小为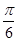 。……14分
。……14分
(1)根据线面平行的判定定理,只要证明
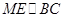 是解决的关键一步。
是解决的关键一步。(2)分别以AB、AC为x、y轴,过A与面ABC垂直的直线为Z
轴建立空间直角坐标系,然后表示直线的方向向量与平面的法向量,进而得到线面角的大小的求解。
解:
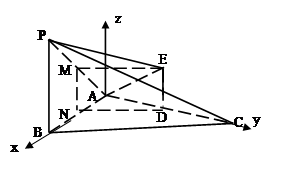
(I)设AP中点为M,AB中点为N,连接EM、DN,
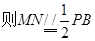 ,
,
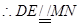 ,
,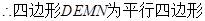 ,
,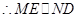 ,……..3分
,……..3分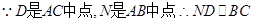 ,由公理4得
,由公理4得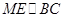 ,
,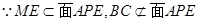
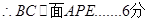
(II)分别以AB、AC为x、y轴,过A与面ABC垂直的直线为Z
轴建立空间直角坐标系…….7分
则B(2,0,0)、C(0,4,0)、P(2,0,2)、
E(0,2,1)
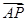 =(2,0,2),
=(2,0,2), =(0,2,1),设F(a,b,0),
=(0,2,1),设F(a,b,0),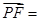 (a-2,b,-2),
(a-2,b,-2),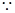 PF
PF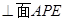 ,
,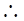
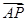
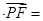 0,得a=4,同理
0,得a=4,同理
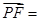 0,得b=1
0,得b=1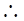 F(4,1,0),…… .9分
F(4,1,0),…… .9分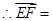 =(4,-1,-1),
=(4,-1,-1),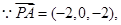
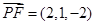
设平面APF法向量为
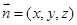 ,由
,由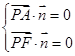 ,得
,得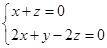 取一组解
取一组解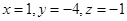 ,
,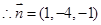 ,……11分
,……11分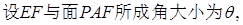
 |cos
|cos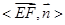 |=
|=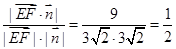 ,
, ,
,  ,直线EF与平面APF所成角大小为
,直线EF与平面APF所成角大小为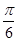 。……14分
。……14分
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
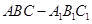 中,侧棱
中,侧棱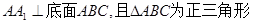 ,点
,点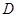 是
是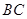 的中点,
的中点,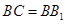 .
.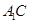 ∥平面
∥平面 ;
;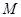 为棱
为棱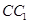 的中点,试证明:
的中点,试证明: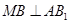 .
.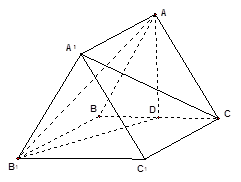
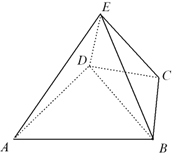
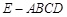 是四棱锥,△
是四棱锥,△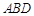 为正三角形,
为正三角形,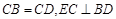 .
.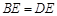 ;
;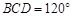 ,M为线段AE的中点,求证:
,M为线段AE的中点,求证: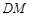 ∥平面
∥平面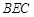 .
.

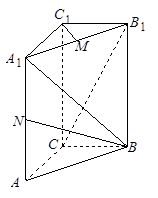
 的长;
的长;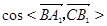 的值;
的值;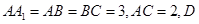 是
是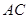 中点.
中点.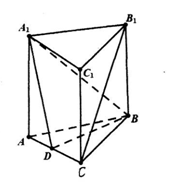
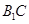 //平面
//平面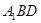 ;
;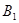 到平面
到平面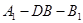 的余弦值.
的余弦值.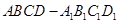 的棱
的棱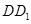 的中点,给出命题
的中点,给出命题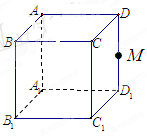
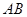 、
、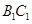 都相交;
都相交;