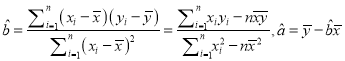题目内容
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)当实数![]() 变化时,求
变化时,求![]() 的最大值;
的最大值;
(3)求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() 有最大值
有最大值![]() ;(3)
;(3)![]() 面积的最大值为
面积的最大值为![]() .
.
【解析】试题分析:⑴由椭圆的离心率是![]() ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为![]() ,列出方程组,求出
,列出方程组,求出![]() 及
及![]() ,由此能求出椭圆
,由此能求出椭圆![]() 的方程;
的方程;
⑵联立直线方程和椭圆方程消去![]() ,求出
,求出![]() 的横坐标,代入直线方程求出对应的纵坐标,代入两点间的距离,求出
的横坐标,代入直线方程求出对应的纵坐标,代入两点间的距离,求出![]() ,
,
⑶求出点![]() 到直线
到直线![]() 的距离
的距离![]() ,从而求得
,从而求得![]() 的面积的表达式,运用不等式计算求得结果
的面积的表达式,运用不等式计算求得结果
解析:(1)由题意得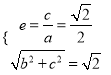 ,得
,得![]() ,从而
,从而![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() ;
;
(2)设![]() ,联立
,联立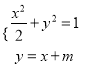 消去
消去![]() ,整理得
,整理得![]() ,
,
由题意知![]() ,
,
所以![]() ,
, ![]() ,
,
所以![]() ,
,
所以当且仅当![]() 时,
时, ![]() 有最大值
有最大值![]() ;
;
(3)点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,从而
,从而![]() 的面积为
的面积为
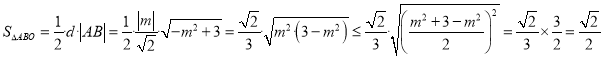 ,
,
(当且仅当![]() ,即
,即![]() 时,等号成立.)
时,等号成立.)
所以![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目