题目内容
2.已知函数f(x)=log2(x+m),且f(0),f(2),f(6)成等差数列,求实数m的值.分析 求出f(0),f(2),f(6),利用等差数列得到方程,即可求出m值.
解答 解:函数f(x)=log2(x+m),f(0)=log2m,f(2)=log2(2+m),f(6)=log2(6+m)成等差数列,
可得:2log2(2+m)=log2m+log2(6+m),
即(2+m)2=m(6+m),解得m=2.
故答案为:2.
点评 本题考查对数运算法则的应用,等差数列的性质的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知0<a<b<1,e是自然对数的底数,则正确的是( )
| A. | ${(\frac{1}{e})^a}<{(\frac{1}{e})^b}$ | B. | 3b<3a | C. | (lga)2<(lgb)2 | D. | loga3>logb3 |
13.已知实数x,y满足x>y,则下列关系式恒成立的是( )
| A. | x3>y3 | B. | x2>y2 | C. | ln(x2+1)>ln(y2+1) | D. | $\frac{1}{{x}^{2}+1}$>$\frac{1}{{y}^{2}+1}$ |
17.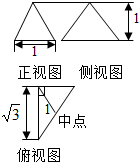 某几何体的三视图如图所示,则它的外接球的体积为( )
某几何体的三视图如图所示,则它的外接球的体积为( )
 某几何体的三视图如图所示,则它的外接球的体积为( )
某几何体的三视图如图所示,则它的外接球的体积为( )| A. | 4π | B. | $\frac{8}{3}π$ | C. | $\frac{4}{9}π$ | D. | $\frac{4}{3}π$ |
11.已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(b>a>0)的正半轴焦点为F,负半轴焦点为F′,AA′为长轴,点Q为椭圆上任意一点,则分别以|QF|,|QF′|,|AA′|为直径的圆之间的位置关系说法正确的是( )
| A. | 以|QF|为直径的圆与以|AA′|为直径的圆内切 | |
| B. | 以|QF′|为直径的圆与以|AA′|为直径的圆相交 | |
| C. | 以|QF|为直径的圆与以|AA′|为直径的圆相交 | |
| D. | 以|QF|为直径的圆与以|QF′|为直径的圆相切 |