题目内容
11.已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(b>a>0)的正半轴焦点为F,负半轴焦点为F′,AA′为长轴,点Q为椭圆上任意一点,则分别以|QF|,|QF′|,|AA′|为直径的圆之间的位置关系说法正确的是( )| A. | 以|QF|为直径的圆与以|AA′|为直径的圆内切 | |
| B. | 以|QF′|为直径的圆与以|AA′|为直径的圆相交 | |
| C. | 以|QF|为直径的圆与以|AA′|为直径的圆相交 | |
| D. | 以|QF|为直径的圆与以|QF′|为直径的圆相切 |
分析 由椭圆的定义可得,|QF+|QF′|=2b,|AA′|=2b,由两圆的位置关系和三角形的中位线定理,即可判断A正确,B,C,D错误.
解答 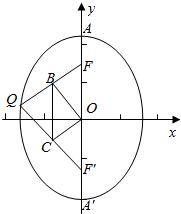 解:由椭圆的定义可得,|QF+|QF′|=2b,|AA′|=2b,
解:由椭圆的定义可得,|QF+|QF′|=2b,|AA′|=2b,
对于A,以|QF|为直径的圆与以|AA′|为直径的圆心距为
|OB|=$\frac{1}{2}$|QF′|=b-$\frac{1}{2}$|QF|,即为两圆内切,故正确;
对于B,以|QF′|为直径的圆与以|AA′|为直径的圆心距为
|OC|=$\frac{1}{2}$|QF|=b-$\frac{1}{2}$|QF'|,即为两圆内切,故不正确;
对于C,由A可得两圆内切,故不正确;
对于D,以|QF|为直径的圆与以|QF'|为直径的圆心距为
|BC|=$\frac{1}{2}$|FF'|=c,而两圆的半径之和为b,两圆相交,故不正确.
故选:A.
点评 本题考查椭圆的定义,考查两圆的位置关系的判断,考查推理能力,属于中档题.

练习册系列答案
相关题目
6.函数f(x)=x2+3x+2在区间(-5,5)上的最大值、最小值分别是( )
| A. | 42,12 | B. | 42,-$\frac{1}{4}$ | ||
| C. | 12,-$\frac{1}{4}$ | D. | 无最大值,有最小值是-$\frac{1}{4}$ |
16.下列表示正确的是( )
| A. | 0∈∅ | B. | 1∈{偶数} | C. | 0∈{x|0<x<4} | D. | 2∈{x|x2-4=0} |
3.三角形的面积为S平方分米,底边长为1.8分米,底边上的高为H分米,则H和S的函数关系式是( )
| A. | S=0.9H(H≥0) | B. | S=0.9H(H>0) | C. | H=$\frac{S}{0.9}$(S≥0) | D. | H=$\frac{S}{0.9}$(S>0) |
 如图所示,正方体ABCD-A′B′C′D′的棱长为a,M是AD的中点,N是BD′上一点,且D′N:NB=1:2,MC与BD交于P,求证:面NPC⊥平面ABCD.
如图所示,正方体ABCD-A′B′C′D′的棱长为a,M是AD的中点,N是BD′上一点,且D′N:NB=1:2,MC与BD交于P,求证:面NPC⊥平面ABCD.