题目内容
7.求方程${x}^{\frac{2}{3}}$=|x|的实根的个数,并指出有哪些实根.分析 根据方程的根与函数零点的关系,将求方程${x}^{\frac{2}{3}}$=|x|的实根的个数的问题转化为求函数y=${x}^{\frac{2}{3}}$与y=|x|的交点个数的关系,作图分析可得答案.
解答 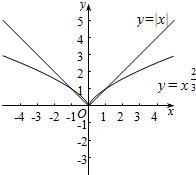 解:方程方程${x}^{\frac{2}{3}}$=|x|的实根个数,即即函数y=${x}^{\frac{2}{3}}$与y=|x|的图象交点的个数,
解:方程方程${x}^{\frac{2}{3}}$=|x|的实根个数,即即函数y=${x}^{\frac{2}{3}}$与y=|x|的图象交点的个数,
故可以将求根个数的问题转化为求两个函数图象的交点个数.
如图在同一坐标系中作出y=${x}^{\frac{2}{3}}$与y=|x|,由图象可以看出两图象只有3个交点,
故方程的实根只有3个.分别为:-1,0,1.
点评 本题主要考查函数零点与方程的根的关系,以及其变式方程的根与两个相关函数交点坐标之间的关系,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
16.下列表示正确的是( )
| A. | 0∈∅ | B. | 1∈{偶数} | C. | 0∈{x|0<x<4} | D. | 2∈{x|x2-4=0} |