题目内容
数列{an}中a1 = 2,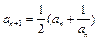 ,{bn}中
,{bn}中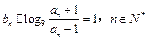 .
.
(1)求证:数列{bn}为等比数列,并求出其通项公式;
(2)当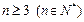 时,证明:
时,证明: .
.
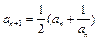 ,{bn}中
,{bn}中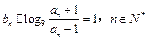 .
.(1)求证:数列{bn}为等比数列,并求出其通项公式;
(2)当
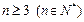 时,证明:
时,证明: .
.(1)证明见解析。
(2)证明见解析。
(2)证明见解析。
证明:(1) 由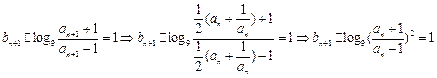
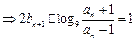 又
又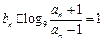 ∴
∴ 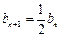
又n = 1时,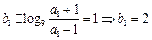
∴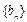 为等比数列,b1 = 2,
为等比数列,b1 = 2,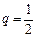 ,∴
,∴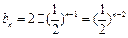
(2) ∵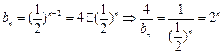 ∴
∴ 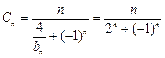
先证: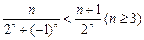
当n为偶数时,显然成立;
当n为奇数时,即证
而当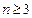 时,
时,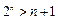 显然也成立,故
显然也成立,故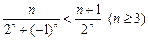
当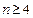 时,令
时,令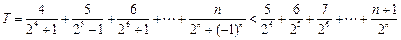
又令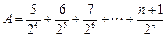 ①
①
 ②
②
①-②: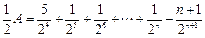
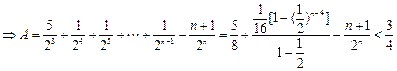
∴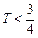
又
∴所证式子左边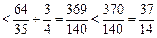
即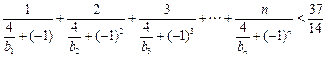
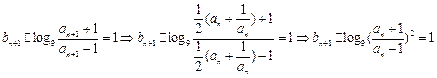
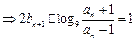 又
又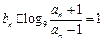 ∴
∴ 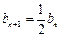
又n = 1时,
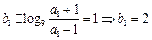
∴
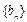 为等比数列,b1 = 2,
为等比数列,b1 = 2,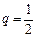 ,∴
,∴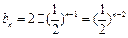
(2) ∵
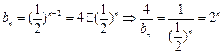 ∴
∴ 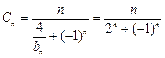
先证:
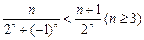
当n为偶数时,显然成立;
当n为奇数时,即证

而当
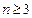 时,
时,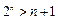 显然也成立,故
显然也成立,故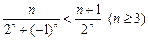
当
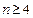 时,令
时,令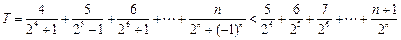
又令
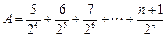 ①
① ②
②①-②:
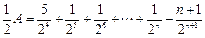
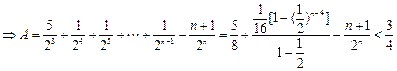
∴
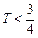
又

∴所证式子左边
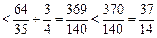
即
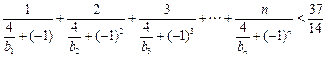

练习册系列答案
相关题目
 (an-1).
(an-1).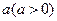 ,公比为
,公比为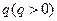 ,前
,前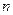 项和为
项和为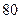 ,其中最大的一项为
,其中最大的一项为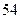 ,又它的前
,又它的前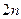 项和为
项和为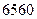 ,求首项
,求首项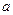 和公比
和公比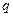 .
.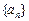 是首项为2,公比为
是首项为2,公比为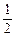 的等比数列,
的等比数列,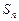 为它的前
为它的前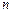 项和.
项和.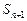 ;
;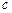 和
和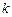 ,使得
,使得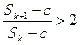 成立.
成立.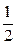
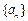 中,
中, ,
,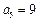 ;数列
;数列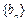 的前
的前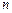 项和是
项和是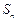 ,且
,且 .
.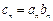 ,求
,求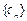 的前n项和
的前n项和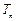 .
.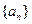 中,
中,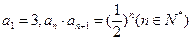 ,则
,则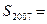 _________________
_________________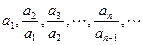 是首项为1,公比为2的等比数列,则a100等于( )
是首项为1,公比为2的等比数列,则a100等于( )