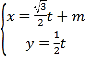题目内容

【题目】已知椭圆的左、右焦点为别为、，且过点和.

（1）求椭圆的标准方程；

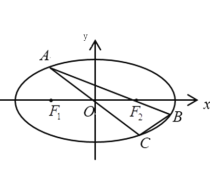
（2）如图，点为椭圆上一动点（非长轴端点），的延长线与椭圆交于点，的延长线与椭圆交于点，求面积的最大值．

【答案】（1）；（2）

【解析】

（1）将点和代入椭圆方程解得，即可得椭圆方程；

（2）当的斜率不存在时，易得；当的斜率存在时，设的方程为，联立，得：，设，利用韦达定理得，则，点到直线的距离是点到直线的距离的2倍，则，得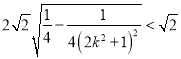；进行比较，得出面积的最大值.

（1）根据题意得，将点和代入椭圆方程得：，

解得：，所以椭圆的方程为.

（2）由（1）得椭圆的，，

①当的斜率不存在时，易知，

；

②当的斜率存在时，设直线的方程为，

联立方程组，消去得：

设，，

，

点到直线的距离，因为是线段的中点，所以点到直线的距离为，

所以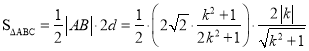

综上，面积的最大值为.

练习册系列答案
相关题目

【题目】定义区间（m，n），，，的长度均为，其中.

（1）若关于x的不等式的解集构成的区间的长度为，求实数a的值；

（2）求关于x的不等式的解集构成的区间的长度的取值范围；

（3）已知关于x的不等式组的解集构成的各区间长度和为5，求实数t的取值范围.

【题目】已知函数f（x），g（x）满足关系g（x）=f（x）f（x+α），其中α是常数．

（1）设f（x）=cosx+sinx，，求g（x）的解析式；

（2）设计一个函数f（x）及一个α的值，使得；

（3）当f（x）=|sinx|+cosx，时，存在x1，x2∈R，对任意x∈R，g（x1）≤g（x）≤g（x2）恒成立，求|x1-x2|的最小值．

【题目】在某次测量中得到的A样本数据如下：82，84，84，86，86，86，88，88，88，88.若B样本数据恰好是A样本数据都加2后所得数据，则A，B两样本的下列数字特征对应相同的是

A. 众数 B. 平均数 C. 中位数 D. 标准差

【题目】某商品销售价格和销售量与销售天数有关，第x天的销售价格（元/百斤），第x天的销售量（百斤）（a为常数），且第7天销售该商品的销售收入为2009元．

（1）求第10天销售该商品的销售收入是多少？

（2）这20天中，哪一天的销售收入最大？为多少？

【题目】对于函数，且的定义域为，．

（1）求实数的值，使函数为奇函数；

（2）在（1）的条件下，令，求使方程，有解的实数的取值范围；

（3）在（1）的条件下，不等式对于任意的恒成立，求实数的取值范围．

【题目】在直角坐标坐标系中，曲线的参数方程为（为参数），以直角坐标系的原点为极点，以轴的正半轴为极轴建立极坐标系，已知直线的极坐标方程为.

（1）求曲线的普通方程；

（2）若与曲线相切，且与坐标轴交于两点，求以为直径的圆的极坐标方程.

【题目】以平面直角坐标系的原点为极点，轴的正半轴为极轴，建立极坐标系，已知直线的参数方程是 (m>0,t为参数)，曲线的极坐标方程为．

（1）求直线的普通方程和曲线的直角坐标方程；

（2）若直线与轴交于点，与曲线交于点，且，求实数的值．

【题目】为了研究学生的数学核心素养与抽象能力(指标)、推理能力(指标)、建模能力(指标)的相关性，将它们各自量化为1、2、3三个等级，再用综合指标的值评定学生的数学核心素养，若，则数学核心素养为一级；若，则数学核心素养为二级；若，则数学核心素养为三级，为了了解某校学生的数学核心素养，调查人员随机访问了某校10名学生，得到如下数据：

学生编号

(1)在这10名学生中任取两人，求这两人的建模能力指标相同条件下综合指标值也相同的概率；

(2)在这10名学生中任取三人，其中数学核心素养等级是一级的学生人数记为，求随机变量的分布列及其数学期望.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网