题目内容
【题目】定义区间(m,n),![]() ,
,![]() ,
,![]() 的长度均为
的长度均为![]() ,其中
,其中![]() .
.
(1)若关于x的不等式![]() 的解集构成的区间的长度为
的解集构成的区间的长度为![]() ,求实数a的值;
,求实数a的值;
(2)求关于x的不等式![]() 的解集构成的区间的长度的取值范围;
的解集构成的区间的长度的取值范围;
(3)已知关于x的不等式组 的解集构成的各区间长度和为5,求实数t的取值范围.
的解集构成的各区间长度和为5,求实数t的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)观察二次项的系数带有字母,需要先对字母进行讨论,当a等于0时,看出合不合题意,![]() 时,方程
时,方程![]() 的两根设为
的两根设为![]() ,根据根与系数之间的关系,写出两根的和与积,表示出区间长度,得到结果(2)根据所给的函数式,利用三角函九公式进行化简求值,根据二次不等式出不等式成立的条件,由此能求出结果(3)先解关于x的不等式组,解出两个不等式的解集,求两个不等式的解集的交集,
,根据根与系数之间的关系,写出两根的和与积,表示出区间长度,得到结果(2)根据所给的函数式,利用三角函九公式进行化简求值,根据二次不等式出不等式成立的条件,由此能求出结果(3)先解关于x的不等式组,解出两个不等式的解集,求两个不等式的解集的交集,![]() ,不等式组的解集的各区间长度和为6,写出不等式组进行讨论,得到结果.
,不等式组的解集的各区间长度和为6,写出不等式组进行讨论,得到结果.
(1)当![]() 时,不等式
时,不等式![]() 的解为
的解为![]() ,不成立;
,不成立;
当![]() 时,方程
时,方程![]() 的两根设为
的两根设为![]() ,则
,则![]() ,
,![]() ,
,
由题意知![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
所以![]() .
.
(2)![]() ,
,
![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() 的解集为
的解集为![]() ,
,
当![]() 时,
时,![]() 的解集为
的解集为![]() ,
,
∴关于x的不等式![]() 的解集构成的区间的长度的取值范围是
的解集构成的区间的长度的取值范围是![]() .
.
(3)先解不等式![]() ,整理,得
,整理,得![]() ,解得
,解得![]() .
.
∴不等式![]() 的解集为
的解集为![]() ,
,
设不等式![]() 的解集为B,不等式组的解集为
的解集为B,不等式组的解集为![]() ,
,
∵关于x的不等式组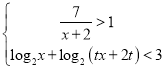 的解集构成的各区间长度和为5,且A∩B(-2,5),
的解集构成的各区间长度和为5,且A∩B(-2,5),
不等式![]() 等价于
等价于 ,
,
当时![]() ,恒成立
,恒成立
当![]() 时,不等式
时,不等式![]() 恒成立,得
恒成立,得![]() ,
,
当![]() 时,不等式
时,不等式![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,
,
∴实数![]() ,
,
综上所述,t的取值范围为![]() .
.

练习册系列答案
相关题目