题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形
为直角梯形![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
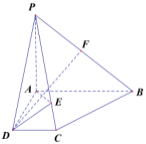
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,且二面角
,且二面角![]() 的正弦值为
的正弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析(2)![]() 或4
或4
【解析】
(1)先证明![]() ,结合
,结合![]() ,推出
,推出![]() 平面
平面![]() ,再根据面面垂直的判定定理证明出结论;
,再根据面面垂直的判定定理证明出结论;
(2)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,利用向量法结合夹角公式建立
轴建立空间直角坐标系,利用向量法结合夹角公式建立![]() 的关系式,求解即可.
的关系式,求解即可.
(1)因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴,建立如图所示的空间直角坐标系:
轴,建立如图所示的空间直角坐标系:

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由(1)知![]() 平面
平面![]() ,故
,故![]() ,
,
又![]() 是
是![]() 的中点,
的中点,![]() ,
,
![]()
![]() ,且
,且![]() ,
,
∴![]() 平面
平面![]() ,
,
∴平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∵![]() ,
,
∴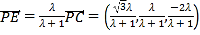 ,
,
∴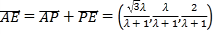 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() 且
且![]() ,
,
∴![]() 且
且![]() ,
,
∴![]() ,令
,令![]() ,则
,则![]() ,
,
∴平面![]() 的一个法向量
的一个法向量![]() ,
,
∵二面角![]() 的正弦值为
的正弦值为![]() ,
,
∴![]() ,
,
∴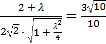 ,
,
∴![]() 或4.
或4.

【题目】2019年第一期中国青年阅读指数数据显示,从阅读需求的角度,排名前三的阅读领域分别为文学、哲学及社会科学和历史.某学校从文科生和理科生中选取了经常阅读的学生进行了假期阅读内容和阅读时间方面的调查,得到以下数据.
学生所学文理与阅读内容列联表
文学阅读人数 | 非文学阅读人数 | 调查人数 | |
理科生 | 70 | 130 | 200 |
文科生 | 45 | 55 | 100 |
合计 | 115 | 185 | 300 |
(Ⅰ)判断能否有![]() 把握认为学生所学文理与阅读内容有关?
把握认为学生所学文理与阅读内容有关?
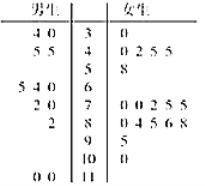
(Ⅱ)从阅读时间大于30分钟的被调查同学中随机选取30名学生,其阅读时间(分钟)整理成如图所示的茎叶图,并绘制日均阅读时间分布表;
其中30名同学的日均阅读时间分布表(单位:分钟)
阅读时间 |
|
|
|
男生人数 | 4 |
| 2 |
女生人数 |
| 10 | 2 |
求出![]() ,
,![]() 的值,并根据日均时间分布表,估计这30名同学日阅读时间的平均值;
的值,并根据日均时间分布表,估计这30名同学日阅读时间的平均值;
(Ⅲ)从(Ⅱ)中日均阅读时间高于90分钟的同学中随机选取2人介绍阅读体会,求这2人性别相同的概率.
参考公式: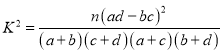 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |