题目内容
【题目】已知定义域为R的函数![]() 是奇函数
是奇函数
(1)求![]() 、
、![]() 的值;
的值;
(2)判断![]() 的单调性(不需要证明),并写出
的单调性(不需要证明),并写出![]() 的值域;
的值域;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 在
在![]() 上单调递增,
上单调递增,![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据奇函数的性质,由![]() ,
,![]() 可求得
可求得![]() 的值;
的值;
(2)根据函数![]() 为增,则
为增,则![]() 为减,
为减,![]() 也为减的性质可得函数
也为减的性质可得函数![]() 的单调性;利用不等式的性质可得
的单调性;利用不等式的性质可得![]() 的值域;
的值域;
(3)根据奇函数的性质,将不等式等价转化为![]() 对任意的
对任意的![]() 恒成立,再利用单调性将不等式进一步转化为
恒成立,再利用单调性将不等式进一步转化为![]() 对任意的
对任意的![]() 恒成立,从而求得
恒成立,从而求得![]() 的取值范围.
的取值范围.
(1)因为函数是定义在![]() 上的奇函数,所以
上的奇函数,所以![]() ,
,
所以![]() ,又
,又![]() .
.
(2)由(1)得![]() ,
,
所以![]() 在
在![]() 上单调递增;
上单调递增;
因为![]()
![]() ,
,
所以![]() 的值域为
的值域为![]() .
.
(3)因为函数![]() 为奇函数,
为奇函数,
所以原不等式![]()
![]()
![]()
![]() 对任意的
对任意的![]() 恒成立,
恒成立,
所以![]() 任意的
任意的![]() 恒成立,
恒成立,
令![]() ,则
,则![]()
所以![]() ,
,
所以![]() .
.

练习册系列答案
相关题目
【题目】支付宝和微信支付是目前市场占有率较高的支付方式,某第三方调研机构对使用这两种支付方式的人数作了对比.从全国随机抽取了100个地区作为研究样本,计算了各个地区样本的使用人数,其频率分布直方图如图.
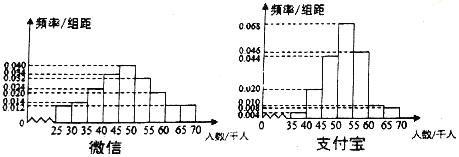
(1)记A表示事件“微信支付人数低于50千人”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为支付人数与支付方式有关;
支付人数<50千人 | 支付人数≥50千人 | 总计 | |
微信支付 | |||
支付宝支付 | |||
总计 |
(3)根据支付人数的频率分布直方图,对两种支付方式的优劣进行比较.
附:
P(K2≥K) | 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
K2=![]()