题目内容
4名师范生分到两所学校实习,若甲、乙不在同一所学校,则不同的分法共有
- A.8种
- B.10种
- C.12种
- D.16种
A
分析:根据题意,分3步进行,首先分配甲,再分配乙,最后分配剩余的两人,依次求得其不同的分配方法数目,进而由分步计数原理计算可得答案.
解答:根据题意,先分配甲,有两种情况;
再分配乙,由于甲、乙不在同一所学校,则乙有1种分配方法;
最后分配剩余的两人,每人有2种方法,则共有2×2=4种不同的方法;
由分步计数原理,可得符合条件的共2×4=8种方法;
故选A.
点评:本题考查排列组合的运用,注意除甲乙之外的两人并没有要求平均分组,应该由分步计数原理来计算其不同的分配方法;这是一个易错点.
分析:根据题意,分3步进行,首先分配甲,再分配乙,最后分配剩余的两人,依次求得其不同的分配方法数目,进而由分步计数原理计算可得答案.
解答:根据题意,先分配甲,有两种情况;
再分配乙,由于甲、乙不在同一所学校,则乙有1种分配方法;
最后分配剩余的两人,每人有2种方法,则共有2×2=4种不同的方法;
由分步计数原理,可得符合条件的共2×4=8种方法;
故选A.
点评:本题考查排列组合的运用,注意除甲乙之外的两人并没有要求平均分组,应该由分步计数原理来计算其不同的分配方法;这是一个易错点.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 个单位长度后得到图象F',若F'的一个对称中心为(
个单位长度后得到图象F',若F'的一个对称中心为( ,0),则φ的一个可能取值是
,0),则φ的一个可能取值是


 终边相同的是
终边相同的是

 如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.
如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.
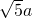
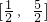
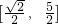
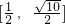
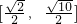
 在其定义域上是减函数
在其定义域上是减函数