题目内容
设0<a<b<1,且a+b=1,给出下列结论:
①log2(b-a)<0②log2a+log2b>-2③log2a>1④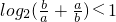
其中正确结论的个数是
- A.1个
- B.2个
- C.3个
- D.4个
A
分析:根据b-a的范围,以及对数的运算性质可判定①的真假,根据对数的运算性质进行化简,然后根据基本不等式求出ab的取值范围,从而可判定②的真假,根据a的范围可判定③的真假,根据基本不等式可求出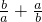 的取值范围,从而可判定④的真假.
的取值范围,从而可判定④的真假.
解答:∵0<a<b<1,∴0<b-a<1,log2(b-a)<log21=0,故①正确;
∵0<a<b<1,且a+b=1,∴a+b=1>2 即ab<
即ab< ,log2a+log2b=log2ab<log2
,log2a+log2b=log2ab<log2 =-2,故②不正确;
=-2,故②不正确;
∵0<a<b<1∴log2a<log21=0,故③不正确;
∵0<a<b<1,且a+b=1∴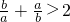 则
则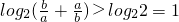 ,故④不正确.
,故④不正确.
故选A.
点评:本题主要考查了基本不等式,以及对数运算性质的综合应用,属于基础题.
分析:根据b-a的范围,以及对数的运算性质可判定①的真假,根据对数的运算性质进行化简,然后根据基本不等式求出ab的取值范围,从而可判定②的真假,根据a的范围可判定③的真假,根据基本不等式可求出
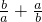 的取值范围,从而可判定④的真假.
的取值范围,从而可判定④的真假.解答:∵0<a<b<1,∴0<b-a<1,log2(b-a)<log21=0,故①正确;
∵0<a<b<1,且a+b=1,∴a+b=1>2
 即ab<
即ab< ,log2a+log2b=log2ab<log2
,log2a+log2b=log2ab<log2 =-2,故②不正确;
=-2,故②不正确;∵0<a<b<1∴log2a<log21=0,故③不正确;
∵0<a<b<1,且a+b=1∴
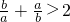 则
则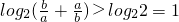 ,故④不正确.
,故④不正确.故选A.
点评:本题主要考查了基本不等式,以及对数运算性质的综合应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
