题目内容
下列说法正确的是
- A.函数
 在其定义域上是减函数
在其定义域上是减函数 - B.两个三角形全等是这两个三角形面积相等的必要条件
- C.命题“?x∈R,x2+x+1>0”的否定是“?x∈R,x2+x+1<0”
- D.给定命题P、q,若P∧q是真命题,则?P是假命题
D
分析:根据题意,依次分析命题:对于A,根据题意,举出反例,有-1<2,则f(-1)<f(2),A错误;对于B,由三角形全等则三角形面积相等,反之三角形面积相等推不出三角形全等,分析可得两个三角形全等是这两个三角形面积相等的充分条件,B错误;对于C,根据命题的否定可得“?x∈R,x2+x+1>0”的否定,C错误;对于D,由P∧q是真命题,可得P为真命题,那么?P是假命题,D正确;即可得答案.
解答:根据题意,依次分析命题:
对于A,对于f(x)= ,有-1<2,则f(-1)<f(2),则该函数不是减函数,A错误;
,有-1<2,则f(-1)<f(2),则该函数不是减函数,A错误;
对于B,若三角形全等则三角形面积相等,反之三角形面积相等推不出三角形全等,则两个三角形全等是这两个三角形面积相等的充分条件,B错误;
对于C,命题“?x∈R,x2+x+1>0”的否定是“?x∈R,x2+x+1≤0”,C错误;
对于D,若P∧q是真命题,则P为真命题,那么?P是假命题,D正确.
故选D.
点评:本题考查命题真假的判断,考查知识点较多,关键是掌握相关的知识点并能根据题意举出反例.
分析:根据题意,依次分析命题:对于A,根据题意,举出反例,有-1<2,则f(-1)<f(2),A错误;对于B,由三角形全等则三角形面积相等,反之三角形面积相等推不出三角形全等,分析可得两个三角形全等是这两个三角形面积相等的充分条件,B错误;对于C,根据命题的否定可得“?x∈R,x2+x+1>0”的否定,C错误;对于D,由P∧q是真命题,可得P为真命题,那么?P是假命题,D正确;即可得答案.
解答:根据题意,依次分析命题:
对于A,对于f(x)=
 ,有-1<2,则f(-1)<f(2),则该函数不是减函数,A错误;
,有-1<2,则f(-1)<f(2),则该函数不是减函数,A错误;对于B,若三角形全等则三角形面积相等,反之三角形面积相等推不出三角形全等,则两个三角形全等是这两个三角形面积相等的充分条件,B错误;
对于C,命题“?x∈R,x2+x+1>0”的否定是“?x∈R,x2+x+1≤0”,C错误;
对于D,若P∧q是真命题,则P为真命题,那么?P是假命题,D正确.
故选D.
点评:本题考查命题真假的判断,考查知识点较多,关键是掌握相关的知识点并能根据题意举出反例.

练习册系列答案
相关题目
 ,则下列说法正确的是( )
,则下列说法正确的是( ) 有且只有一个零点
B.
有且只有一个零点
B. ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
 ,乙比甲成绩稳定,应该选乙参加比赛
,乙比甲成绩稳定,应该选乙参加比赛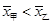 ,甲比乙成绩稳定,应该选甲参加比赛
,甲比乙成绩稳定,应该选甲参加比赛 :函数
:函数 (
( 且
且 )的图像恒过点
)的图像恒过点 ;
; :函数
:函数 有两个零点.
有两个零点.  为假命题 D.
为假命题 D. 为真命题
为真命题 的导函数
的导函数 的图象如上图所示,则下列说法正确的是 ( )
的图象如上图所示,则下列说法正确的是 ( ) 内单调递减 B、函数
内单调递减 B、函数 内单调递增
内单调递增 处取极大值 D、函数
处取极大值 D、函数 处取极小值
处取极小值