题目内容
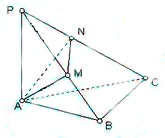
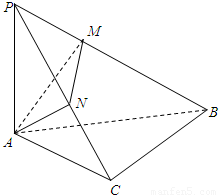
 如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.
如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.
(1)求证:BC⊥面PAC;
(2)求证:PB⊥面AMN.
证明:(1)∵PA⊥平面ABC,BC?平面ABC.
∴PA⊥BC,又AB为斜边,
∴BC⊥AC,PA∩AC=A,∴BC⊥平面PAC.
(2)∵BC⊥平面PAC,AN?平面PAC
∴BC⊥AN,又AN⊥PC,且BC∩PC=C,
∴AN⊥面PBC,又PB?平面PBC.∴AN⊥PB,
又∵PB⊥AM,AM∩AN=A,∴PB⊥平面AMN.
分析:(1)由结论联想判定定理,要证明BC⊥平面PAC,需证明BC垂直于平面PAC中的两条相交直线.已知BC⊥AC,尚缺条件PA⊥BC.于是考虑从其它条件所具备的性质中去寻找.
(2)欲证PB⊥平面AMN,根据直线与平面垂直的判定定理可知只需证PB与平面AMN内两相交直线垂直,根据线面垂直的判定定理可知AN⊥面PBC,从而AN⊥PB,又PB⊥AM,AM∩AN=A,满足定理所需条件.
点评:本题主要考查了直线与平面垂直的判定.应熟练记忆直线与平面垂直的判定定理,同时考查了空间想象能力,属于基础题之列.
∴PA⊥BC,又AB为斜边,
∴BC⊥AC,PA∩AC=A,∴BC⊥平面PAC.
(2)∵BC⊥平面PAC,AN?平面PAC
∴BC⊥AN,又AN⊥PC,且BC∩PC=C,
∴AN⊥面PBC,又PB?平面PBC.∴AN⊥PB,
又∵PB⊥AM,AM∩AN=A,∴PB⊥平面AMN.
分析:(1)由结论联想判定定理,要证明BC⊥平面PAC,需证明BC垂直于平面PAC中的两条相交直线.已知BC⊥AC,尚缺条件PA⊥BC.于是考虑从其它条件所具备的性质中去寻找.
(2)欲证PB⊥平面AMN,根据直线与平面垂直的判定定理可知只需证PB与平面AMN内两相交直线垂直,根据线面垂直的判定定理可知AN⊥面PBC,从而AN⊥PB,又PB⊥AM,AM∩AN=A,满足定理所需条件.
点评:本题主要考查了直线与平面垂直的判定.应熟练记忆直线与平面垂直的判定定理,同时考查了空间想象能力,属于基础题之列.

练习册系列答案
相关题目
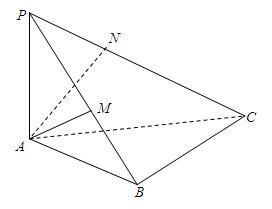 21、如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.
21、如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.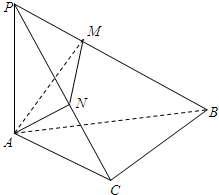 如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,
如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,