题目内容
用数学归纳法证明对任何正整数n有
+
+
+
+…+
=
.
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 35 |
| 1 |
| 63 |
| 1 |
| 4n2-1 |
| n |
| 2n+1 |
证明:①当n=1时,左边=
,右边=
=
,
∴等式成立;
②假设当n=k(k≥1,k∈N*)时等式成立,即
+
+
+
+…+
=
,
则当n=k+1时,
+
+
+
+…+
+
=
+
=
+
=
=
=
.
∴当n=k+1时等式也成立.
由①②知等式对任何正整数n都成立.
| 1 |
| 3 |
| 1 |
| 2+1 |
| 1 |
| 3 |
∴等式成立;
②假设当n=k(k≥1,k∈N*)时等式成立,即
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 35 |
| 1 |
| 63 |
| 1 |
| 4k2-1 |
| k |
| 2k+1 |
则当n=k+1时,
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 35 |
| 1 |
| 63 |
| 1 |
| 4k2-1 |
| 1 |
| 4(k+1)2-1 |
=
| k |
| 2k+1 |
| 1 |
| 4(k+1)2-1 |
=
| k |
| 2k+1 |
| 1 |
| (2k+3)(2k+1) |
=
| 2k2+3k+1 |
| (2k+3)(2k+1) |
=
| (k+1)(2k+1) |
| (2k+3)(2k+1) |
=
| k+1 |
| 2(k+1)+1 |
∴当n=k+1时等式也成立.
由①②知等式对任何正整数n都成立.

练习册系列答案
相关题目
 是
是 的共轭复数. 若
的共轭复数. 若 ,
, (
( 为虚数单位),则
为虚数单位),则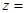 ( )
( )



 满足
满足 (
( 为虚数单位),则
为虚数单位),则 为 .
为 . 都是偶数”,正确的反设为(***)
都是偶数”,正确的反设为(***) (
( 是虚数单位),则
是虚数单位),则 = .
= .