题目内容
(本小题满分12分)求通过原点且与两直线l1:x+2y-9=0,l2:2x-y+2=0相切的圆的方程
解:∵圆与l1、l2相切,故圆心的轨迹在l1与l2的夹角平分线上.
∵k1=-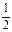 ,k2=2,k1·k2=-1,∴l1⊥l2. …………………………………4分
,k2=2,k1·k2=-1,∴l1⊥l2. …………………………………4分
设l1与l2的夹角平分线为l,其斜率为k,故l与l2夹角为45°.
∴|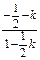 |=1.∴k=-3或k=
|=1.∴k=-3或k=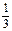 (舍去). …………………………………6分
(舍去). …………………………………6分
l:3x+y-7=0,设圆心(a,b),则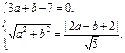 解得
解得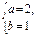 或
或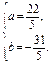
故圆方程为(x-2)2+(y-1)2=5或(x-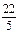 )2+(y+
)2+(y+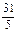 )2=
)2=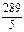 .………………………………12分
.………………………………12分
∵k1=-
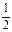 ,k2=2,k1·k2=-1,∴l1⊥l2. …………………………………4分
,k2=2,k1·k2=-1,∴l1⊥l2. …………………………………4分设l1与l2的夹角平分线为l,其斜率为k,故l与l2夹角为45°.
∴|
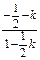 |=1.∴k=-3或k=
|=1.∴k=-3或k=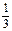 (舍去). …………………………………6分
(舍去). …………………………………6分l:3x+y-7=0,设圆心(a,b),则
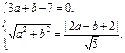 解得
解得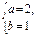 或
或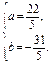
故圆方程为(x-2)2+(y-1)2=5或(x-
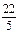 )2+(y+
)2+(y+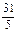 )2=
)2=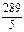 .………………………………12分
.………………………………12分略

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
 是单位圆与
是单位圆与 轴正半轴的交点,
轴正半轴的交点,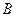 ,
,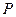 为单位圆上不同的点,
为单位圆上不同的点,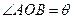 ,
,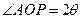 ,
,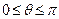 ,
,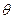 为何值时,
为何值时,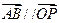 ?
?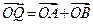 ,则当
,则当 在单位圆上?
在单位圆上?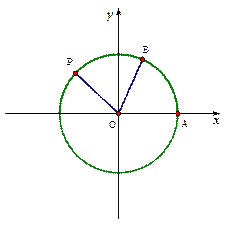
 中,以
中,以 为圆心的圆与直线
为圆心的圆与直线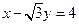 相切。圆
相切。圆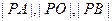 成等比数列,
成等比数列,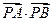 的范围.
的范围.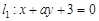 与直线
与直线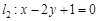 垂直,则
垂直,则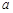 的值为( )
的值为( )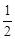
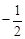
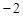
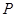 在⊙O外,
在⊙O外,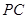 切⊙O于
切⊙O于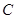 ,
,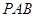 交⊙O于
交⊙O于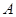 、
、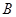 ,则( )
,则( )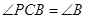
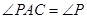
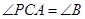
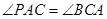
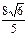 ,则圆的方程为( )
,则圆的方程为( )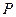 在直线
在直线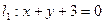 上,过点
上,过点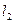 与曲线
与曲线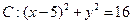 只有一个公共点
只有一个公共点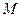 ,则
,则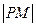 的最小值为__________
的最小值为__________