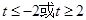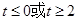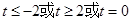题目内容
偶函数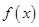 在
在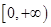 上为减函数,不等式
上为减函数,不等式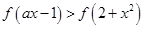 恒成立,则
恒成立,则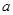 的取值范围是( )
的取值范围是( )
A.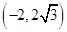 | B.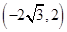 | C.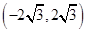 | D.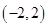 |
D.
解析试题分析:由已知得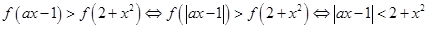 ,当
,当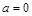 时,显然成立;当
时,显然成立;当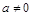 时,在同一坐标系内画函数
时,在同一坐标系内画函数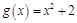 与
与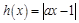 的图像,可得当
的图像,可得当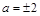 时,
时,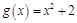 与
与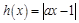 相切,此时的
相切,此时的 值也可令方程
值也可令方程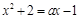 的
的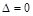 得到.故当
得到.故当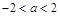 时,函数
时,函数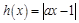 的图像恒在函数
的图像恒在函数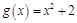 的图像下方,从而
的图像下方,从而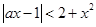 ,即
,即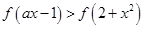 恒成立,故选D.
恒成立,故选D.
考点:1.函数的单调性、奇偶性;2.含参数不等式中的参数取值范围问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数中,既是偶函数又在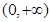 单调递增的函数是( )
单调递增的函数是( )
A.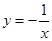 | B.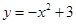 | C.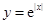 | D.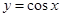 |
如果函数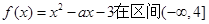 上单调递减,则实数
上单调递减,则实数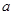 满足的条件是( )
满足的条件是( )
A.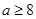 | B.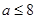 | C.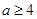 | D.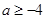 |
函数 是( )
是( )
A.奇函数且在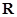 上是减函数 上是减函数 | B.奇函数且在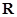 上是增函数 上是增函数 |
C.偶函数且在 上是减函数 上是减函数 | D.偶函数且在 上是增函数 上是增函数 |
已知定义在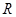 上的函数
上的函数 ,对任意
,对任意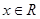 ,都有
,都有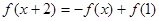 成立,若函数
成立,若函数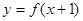 的图象关于点
的图象关于点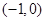 对称,则
对称,则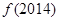 =( )
=( )
| A.0 | B.2014 | C.3 | D.—2014 |
已知幂函数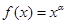 (
(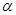 为常数)的图像过点P(2,),则f(x)的单调递减区间是
为常数)的图像过点P(2,),则f(x)的单调递减区间是
| A.(-∞,0) | B.(-∞,+∞) |
| C.(-∞,0)∪(0,+∞) | D.(-∞,0),(0,+∞) |
已知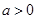 ,函数
,函数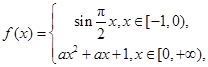 若
若 ,则实数
,则实数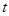 的取值范围为( )
的取值范围为( )
A.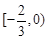 | B.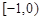 | C.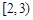 | D.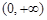 |
若函数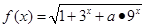 ,其定义域为
,其定义域为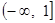 ,则
,则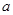 的取值范围是( )
的取值范围是( )
A.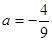 | B.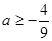 | C.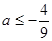 | D.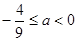 |
 在区间
在区间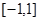 上是增函数,且
上是增函数,且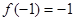 ,当
,当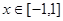 时,函数
时,函数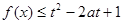 对一切
对一切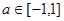 恒成立,则实数
恒成立,则实数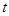 的取值范围是 ( )
的取值范围是 ( )