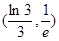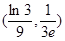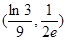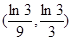题目内容
下列函数中,既是偶函数又在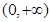 单调递增的函数是( )
单调递增的函数是( )
A.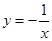 | B.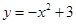 | C.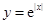 | D.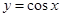 |
C
解析试题分析:分析可知函数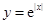 既是偶函数又在
既是偶函数又在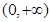 单调递增.
单调递增.
考点:函数的性质.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
若函数 ,则函数
,则函数 ( )
( )
A.是奇函数,在 是增函数 是增函数 | B.是偶函数,在 是减函数 是减函数 |
C.是偶函数,在 是增函数 是增函数 | D.是奇函数,在 是减函数 是减函数 |
设函数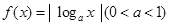 的定义域为
的定义域为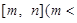
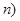 ,值域为
,值域为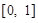 ,若
,若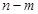 的最小值为
的最小值为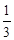 ,则实数a的值为( )
,则实数a的值为( )
A.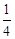 | B.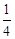 或 或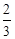 | C.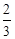 | D.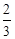 或 或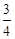 |
函数 的定义域是 ( )
的定义域是 ( )
A.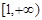 | B.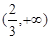 | C.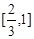 | D.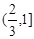 |
已知 为偶函数,且
为偶函数,且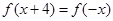 ,当
,当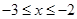 时,
时,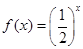 ,则
,则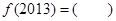
A.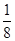 | B. | C.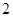 | D.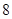 |
函数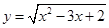 的定义域是( )
的定义域是( )
A.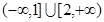 | B. | C.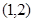 | D. |
已知 是函数f(x)=lnx-(
是函数f(x)=lnx-(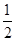 )x的零点,若
)x的零点,若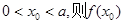 的值满足( )
的值满足( )
A.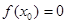 | B.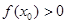 |
C.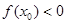 | D.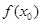 的符号不确定 的符号不确定 |
偶函数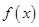 在
在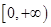 上为减函数,不等式
上为减函数,不等式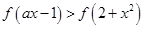 恒成立,则
恒成立,则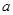 的取值范围是( )
的取值范围是( )
A.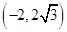 | B.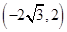 | C.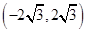 | D.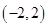 |

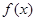 满足
满足 ,当
,当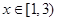 ,
,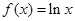 ,若在区间
,若在区间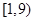 内,函数
内,函数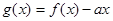 有三个不同零点,则实数
有三个不同零点,则实数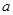 的取值范围是( )
的取值范围是( )