题目内容
【题目】已知点![]() 为椭圆C:
为椭圆C:![]() (
(![]() ,
,![]() )上一点,
)上一点,![]() 和
和![]() 分别为椭圆C的左右焦点,点D为椭圆C的上顶点,且
分别为椭圆C的左右焦点,点D为椭圆C的上顶点,且![]() .
.
(1)椭圆C的方程;
(2)若点A、B、P为椭圆C上三个不同的动点,且满足![]() ,直线
,直线![]() 与直线
与直线![]() 交于点Q,试判断动点Q的轨迹与直线
交于点Q,试判断动点Q的轨迹与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(1)![]() ;(2)相切,理由见解析.
;(2)相切,理由见解析.
【解析】
(1)由已知化简可得![]() ,
,![]() 代入椭圆方程,计算即可求得结果;
代入椭圆方程,计算即可求得结果;
(2)设![]() ,
,![]() ,由
,由![]() 化简可得
化简可得![]() ,利用轨迹法可求得Q的轨迹方程,设直线
,利用轨迹法可求得Q的轨迹方程,设直线![]() 与直线
与直线![]() 交于点M,则点M为线段
交于点M,则点M为线段![]() 的中点,根据
的中点,根据![]() 可求得
可求得![]() ,利用点差法可求得直线直线
,利用点差法可求得直线直线![]() 的方程,和Q的轨迹方程联立,点
的方程,和Q的轨迹方程联立,点![]() 坐标代入化简利用判别式可得出结论相切.
坐标代入化简利用判别式可得出结论相切.
解:(1)由已知可得:![]() ,则
,则![]()
所以 ![]() ,
,![]() ,
,
又由于已知点![]() 在椭圆C上,则
在椭圆C上,则![]() ,解得
,解得![]() ,
,![]() ,
,
椭圆C的方程![]() .
.
(2)设![]() ,
,![]()
∵![]() ,直线
,直线![]() 与直线
与直线![]() 交于点Q,
交于点Q,
∴![]() .
.
则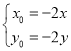 .
.
由![]() ,得
,得![]() ,
,
∴动点Q的轨迹方程为![]() .
.
设直线![]() 与直线
与直线![]() 交于点M,则点M为线段
交于点M,则点M为线段![]() 的中点,且
的中点,且![]() ,
,
当![]() 时,∵
时,∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,整理得
,整理得![]() .
.
将![]() 代入动点Q的轨迹方程得,
代入动点Q的轨迹方程得,![]() .
.
将![]() 代入(※),整理得
代入(※),整理得![]() .
.
∵![]() ,∴直线
,∴直线![]() 与动点Q的轨迹相切.
与动点Q的轨迹相切.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,∴直线
,∴直线![]() 与动点Q的轨迹相切.
与动点Q的轨迹相切.
综上可知,直线![]() 与动点Q的轨迹相切.
与动点Q的轨迹相切.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
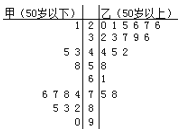
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |