题目内容
研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用,所谓“刹车距离”就是指行驶中的汽车,从刹车开始到停止,由于惯性的作用而又继续向前滑行的一段距离.为了测定某种型号汽车的刹车性能(车速不超过140km/h),对这种汽车进行测试,测得的数据如表:
(1)以车速为x轴,以刹车距离为y轴,在给定坐标系中画出这些数据的散点图;
(2)观察散点图,估计函数的类型,并确定一个满足这些数据的函数表达式;
(3)该型号汽车在国道上发生了一次交通事故,现场测得刹车距离为46.5m,请推测刹车时的速度为多少?请问在事故发生时,汽车是超速行驶还是正常行驶?
| 刹车时的车速(km/h) | 0 | 10 | 20 | 30 | 40 | 50 | 60 |
| 刹车距离(m) | 0 | 0.3 | 1.0 | 2.1 | 3.6 | 5.5 | 7.8 |
(2)观察散点图,估计函数的类型,并确定一个满足这些数据的函数表达式;
(3)该型号汽车在国道上发生了一次交通事故,现场测得刹车距离为46.5m,请推测刹车时的速度为多少?请问在事故发生时,汽车是超速行驶还是正常行驶?

(1)解如图所示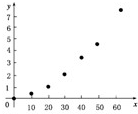
(2)2)根据图象可估计为抛物线.
∴设y=ax2+bx+c.
把表内前三对数代入函数,可得
解得:
∴y=0.002x2+0.01x(0≤x≤140).
经检验,其他各数均满足函数(或均在函数图象上);
(3)当y=46.5时,46.5=0.002x2+0.01x.
整理可得x2+5x-23250=0.
解之得x1=150,x2=-155(不合题意,舍去).
所以可以推测刹车时的速度为150千米/时.
∵150>140,
∴汽车发生事故时超速行驶.汽车属于超速行驶.

(2)2)根据图象可估计为抛物线.
∴设y=ax2+bx+c.
把表内前三对数代入函数,可得
|
解得:
|
∴y=0.002x2+0.01x(0≤x≤140).
经检验,其他各数均满足函数(或均在函数图象上);
(3)当y=46.5时,46.5=0.002x2+0.01x.
整理可得x2+5x-23250=0.
解之得x1=150,x2=-155(不合题意,舍去).
所以可以推测刹车时的速度为150千米/时.
∵150>140,
∴汽车发生事故时超速行驶.汽车属于超速行驶.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
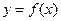 存在反函数
存在反函数 ,若函数
,若函数 的图象经过点
的图象经过点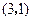 ,则函数
,则函数
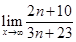 = .
= .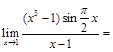 ( )
( )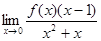 存在,则
存在,则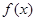 不可能为( )
不可能为( )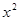 ;
;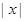 ;
; 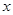 ;
; 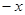 ;
;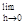
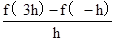 =( )
=( )