题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,对于任意
时,对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)见解析;(2)3
【解析】
(1)分类讨论,求得函数的导数,利用导数与单调性的关系,即可求解;
(2)把对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() ,转化为
,转化为![]() ,结合函数的单调性,分类讨论,即可求解.
,结合函数的单调性,分类讨论,即可求解.
(1)由题意,函数![]() ,
,
当![]() 时,
时,![]() ,则
,则![]()
由![]() ,则
,则![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,则
,则![]() ,
,
由![]() ,令
,令![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
当![]() 时,即
时,即![]() 时,
时,
函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调单调区间为
,单调单调区间为![]() ;
;
当![]() 时,即
时,即![]() ,
,
函数![]() 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为![]() .
.
(2)由对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() ,
,
等价于![]() ,
,
由(1)得,当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() 在
在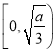 上单调递减,在
上单调递减,在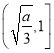 上单调递增,
上单调递增,
所以![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,得
,得![]() (舍去);
(舍去);
当![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,
,
其中![]() ,而
,而![]() ,所以无解,舍去.
,所以无解,舍去.
综上所述,![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
(2)司机师傅小李准备在一辆开了![]() 年的
年的![]() 型车和一辆开了
型车和一辆开了![]() 年的
年的![]() 型车中选择,为了尽最大可能实现
型车中选择,为了尽最大可能实现![]() 年内(含
年内(含![]() 年)不换车,试通过计算说明,他应如何选择.
年)不换车,试通过计算说明,他应如何选择.
附: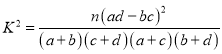 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |