题目内容
【题目】设函数 ![]() 的定义域为
的定义域为 ![]() ,若函数
,若函数 ![]() 满足下列两个条件,则称
满足下列两个条件,则称 ![]() 在定义域
在定义域 ![]() 上是闭函数.①
上是闭函数.① ![]() 在
在 ![]() 上是单调函数;②存在区间
上是单调函数;②存在区间 ![]() ,使
,使 ![]() 在
在 ![]() 上值域为
上值域为 ![]() .如果函数
.如果函数 ![]() 为闭函数,则
为闭函数,则 ![]() 的取值范围是.
的取值范围是.
【答案】![]()
【解析】若函数f(x)= ![]() 为闭函数,则存在区间[a,b],在区间[a,b]上,函数f(x)的值域为[a,b],即
为闭函数,则存在区间[a,b],在区间[a,b]上,函数f(x)的值域为[a,b],即 ![]() ∴a,b是方程x=
∴a,b是方程x= ![]() 的两个实数根, 即a,b是方程x2-(2k+2)x+k2-1=0(x≥
的两个实数根, 即a,b是方程x2-(2k+2)x+k2-1=0(x≥ ![]() ,x≥k)的两个不相等的实数根, 当k≤
,x≥k)的两个不相等的实数根, 当k≤ ![]() 时,
时, 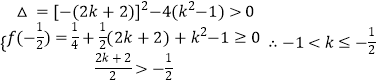
当 ![]() 时,
时, 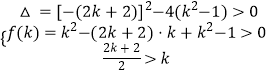 解得
解得 ![]() 无解
无解
综上,可得-1<k ![]()
故答案为 :![]()
先要弄清楚新定义的闭函数的含义,由于函数f(x)是增函数,则问题等价于f(x)=x有两个不等实根,利用二次方程实根的分布求k的范围.

练习册系列答案
相关题目